ΚΥΜΑΤΟΣΥΝΑΡΤΗΣΗ ΚΑΙ ΕΞΙΣΩΣΗ SCHRODINGER (ΣΡΕΝΤΙΝΓΚΕΡ)
ΕΞΙΣΩΣΗ SCHRODINGER (ΣΡΕΝΤΙΝΓΚΕΡ)
Πώς βρίσκουμε όμως μία κυματοσυνάρτηση;
ΕΙΣΑΓΩΓΗ
Είδαμε ότι ένα υποατομικό σωματίδιο,για παράδειγμα ένα ηλεκτρόνιο,δε μπορεί να περιγραφεί σαν υλικό σημείο,με τρεις συντεταγμένες στο χώρο.Υπό ορισμένες συνθήκες συμπεριφέρεται σαν κύμα.
Για την περιγραφή του χρειαζόμαστε μία κυματοσυνάρτηση σε αναλογία με την εξίσωση κύματος που χρησιμοποιούμε για την περιγραφή ενός μηχανικού ή ενός ηλεκτρομαγνητικού κύματος.Την κυματοσυνάρτηση αυτή θα τη συμβολίζουμε με Ψ.
ΚΥΜΑΤΟΣΥΝΑΡΤΗΣΗ
Είδαμε ότι ένα υποατομικό σωματίδιο,για παράδειγμα ένα ηλεκτρόνιο,δε μπορεί να περιγραφεί σαν υλικό σημείο,με τρεις συντεταγμένες στο χώρο.Υπό ορισμένες συνθήκες συμπεριφέρεται σαν κύμα.
Για την περιγραφή του χρειαζόμαστε μία κυματοσυνάρτηση σε αναλογία με την εξίσωση κύματος που χρησιμοποιούμε για την περιγραφή ενός μηχανικού ή ενός ηλεκτρομαγνητικού κύματος.Την κυματοσυνάρτηση αυτή θα τη συμβολίζουμε με Ψ.
ΚΥΜΑΤΟΣΥΝΑΡΤΗΣΗ
Η κυματοσυνάρτηση είναι μία συνάρτηση της θέσης και του χρόνου.
Ψ=ψ(x,y.z,i)
Ψ=ψ(x,y.z,i)
Στα μηχανικά κύματα η εξίσωση κύματος μας δίνει για κάθε χρονική στιγμή τη θέση κάθε σημείου του υλικού μέσου στο οποίο διαδίδεται το κύμα.Στα ηλεκτρομαγνητικά κύματα οι εξισώσεις κύματος που τα περιγράφουν μας δίνουν για κάθε χρονική στιγμή την τιμή της έντασης του ηλεκτρικού και του μαγνητικού πεδίου σε κάθε σημείο του χώρου στον οποίο διαδίδεται το κύμα.
Η κυματοσυνάρτηση Τ όμως που περιγράφει ένα σωματίδιο-κύμα δεν σχετίζεται με κάποιο μέσον διάδοσης ούτε με κάποιες ιδιότητες του χώρου.Είναι δύσκολο να της αποδώσουμε κάποια φυσική σημασία.Μπορούμε μόνο να περιγράψουμε πώς σχετίζεται με τα φυσικά παρατηρούμενα φαινόμενα.
Η κυματοσυνάρτηση Τ όμως που περιγράφει ένα σωματίδιο-κύμα δεν σχετίζεται με κάποιο μέσον διάδοσης ούτε με κάποιες ιδιότητες του χώρου.Είναι δύσκολο να της αποδώσουμε κάποια φυσική σημασία.Μπορούμε μόνο να περιγράψουμε πώς σχετίζεται με τα φυσικά παρατηρούμενα φαινόμενα.
Για κάποιο συγκεκριμένο σημείο,ορισμένη χρονική στιγμή η κυματοσυνάρτηση θα έχει μια συγκεκριμένη τιμή.
Ο Max Born πρότεινε να ερμηνεύσουμε το τετράγωνο του μέτρου της κυματοσυνάρτησης σαν την πιθανότητα θέσης ανά μονάδα όγκου.Δηλαδή, αν ορίσουμε έναν στοιχειώδη όγκο dV γύρω από ένα συγκεκριμένο σημείο (x,y,z) το γινόμενο |Ψ|2dV δίνει την πιθανότητα να βρίσκεται το σωμάτιο μέσα στον όγκο dV στη δεδομένη χρονική στιγμή.
 |
| Απεικόνιση μιας κυματοσυνάρτησης |
H συνάρτηση που αντιστοιχεί σε ένα κβαντικό σύστημα ονομάζεται κυματοσυνάρτηση,επειδή είναι ανάλογη με τις συναρτήσεις που περιγράφουν την εξέλιξη των κυμάτων στην κλασική φυσική.Σε κάθε φυσικό σύστημα,μπορούμε να παρατηρήσουμε κάποια χαρακτηριστικά του φυσικά μεγέθη,π.χ. ταχύτητα,θέση,ορμή.H ψ υπολογίζεται από την εξίσωση του Schrodinger και μας δίνει την δυνατότητα να τα υπολογίσουμε.Υπάρχει μία ψ για κάθε κατάσταση του κβαντικού μας συστήματος και αντίστροφα για κάθε ψ αντιστοιχεί μία κατάσταση του συστήματος.Γνωρίζοντας την ψ ενός συστήματος μπορούμε να υπολογίσουμε όλα τα χαρακτηριστικά μεγέθη του συστήματος και τον τρόπο με τον όποιο αυτά εξελίσσονται στον χρόνο.Η ψ περιλαμβάνει όλη την πληροφορία την οποία μπορούμε να ανακτήσουμε από το σύστημα μας.
ΣΥΝΘΗΚΗ ΚΑΝΟΝΙΚΟΠΟΙΗΣΕΩΣΟ Max Born πρότεινε να ερμηνεύσουμε το τετράγωνο του μέτρου της κυματοσυνάρτησης σαν την πιθανότητα θέσης ανά μονάδα όγκου.Δηλαδή, αν ορίσουμε έναν στοιχειώδη όγκο dV γύρω από ένα συγκεκριμένο σημείο (x,y,z) το γινόμενο |Ψ|2dV δίνει την πιθανότητα να βρίσκεται το σωμάτιο μέσα στον όγκο dV στη δεδομένη χρονική στιγμή.
Αν χωρίσουμε το σύνολο του χώρου σε στοιχειώδεις όγκους dV και σε κάθε σημείο του χώρου βρούμε την τιμή της Ψ για κάποια χρονική στιγμή το άθροισμα των |Ψ|2dV πρέπει να είναι ίσο με τη μονάδα.
Σ|Ψ|2dV=1
Σ|Ψ|2dV=1
Δηλαδή η πιθανότητα να βρίσκεται το σωματίδιο κάπου στο χώρο είναι ίση με τη μονάδα.Με απλά λόγια κάθε χρονική στιγμή το σωματίδιο σίγουρα βρίσκεται κάπου.
Η παραπάνω σχέση προκύπτει από την διάσταση που έδωσε ο Born στο |Ψ|2 και ονομάζεται συνθήκη κανονικοποιήσεως.Εάν η κυματοσυνάρτηση είναι σωστή πρέπει να ικανοποιεί τη συνθήκη κανονικοποιήσεως.
Λόγω του ότι είναι βέβαιο γεγονός ότι θα βρούμε ένα σωμάτιο που μελετούμε κάπου στο χώρο, θα πρέπει η συνολική πιθανότητα να βρούμε το σωματίδιο σε ολόκληρο το χώρο να ισούται με μονάδα.Μαθηματικά,αυτό μεταφράζεται στην απαίτηση:
.png) |
| Αν ορίσουμε έναν στοιχειώδη όγκο dV γύρω από ένα συγκεκριμένο σημείο (x,y,z) το γινόμενο |Ψ|2dV δίνει την πιθανότητα να βρίσκεται το σωμάτιο μέσα στον όγκο dV στη δεδομένη χρονική στιγμή |
Λόγω του ότι είναι βέβαιο γεγονός ότι θα βρούμε ένα σωμάτιο που μελετούμε κάπου στο χώρο, θα πρέπει η συνολική πιθανότητα να βρούμε το σωματίδιο σε ολόκληρο το χώρο να ισούται με μονάδα.Μαθηματικά,αυτό μεταφράζεται στην απαίτηση:
όπου η ολοκλήρωση γίνεται πάνω σε ολόκληρο το χώρο.
Έτσι αν το ολοκλήρωμα μίας κυματοσυνάρτησης είναι πεπερασμένο (δεν απειρίζεται,ή πιο αυστηρά είναι τετραγωνικά ολοκληρώσιμη) και ίσο με τη μονάδα με μία σταθερά Μ≠1,αρκεί για να βρούμε την κυματοσυνάρτηση ενός συστήματος να διαιρέσουμε την κυματοσυνάρτηση αυτή με Μ.
Δηλαδή αν:
τότε:
όπου:
ΨM η μη κανονικοποιημένη κυματοσυνάρτηση.
ΕΞΙΣΩΣΗ SCHRODINGER (ΣΡΕΝΤΙΝΓΚΕΡ)
Πώς βρίσκουμε όμως μία κυματοσυνάρτηση;
Την απάντηση έδωσε ο Erwin Schrodinger διατυπώνοντας την περίφημη εξίσωσή του της οποίας λύση είναι η Ψ .
Για ένα σωματίδιο που κινείται πάνω στον άξονα των x σε μία περιοχή όπου υπάρχει ένα συντηρητικό πεδίο, για κάποια συγκεκριμένη χρονική στιγμή η εξίσωση Schrodinger έχει τη μορφή :
όπου:
ħ (διαβάζεται h-bar) η συντομογραφία του h/2π.
ħ (διαβάζεται h-bar) η συντομογραφία του h/2π.
m η μάζα ηρεμίας του σωματιδίου,
d2Ψ(x) /dx2 η δεύτερη παράγωγος της κυματοσυνάρτησης ως προς x,
d2Ψ(x) /dx2 η δεύτερη παράγωγος της κυματοσυνάρτησης ως προς x,
U(x) η δυναμική ενέργεια του σωματιδίου λόγω της θέσης του,
E η ολική ενέργεια του σωματιδίου.
Η λύση της εξίσωσης αυτής είναι η κυματοσυνάρτηση του σωματιδίου.
Εφόσον το σωματίδιο είναι περιορισμένο να κινείται πάνω στον άξονα των x η κυματοσυνάρτησή του πρέπει να ικανοποιεί τη συνθήκη |Ψ|2dV=1 δηλαδή το σωμάτιο σίγουρα βρίσκεται κάπου στον άξονα των x.
Στην κλασική φυσική η αντίστοιχη εξίσωση με αυτήν του Schrodinger είναι η εξίσωση κίνησης του Νεύτωνα.Από αυτήν παίρνουμε αριθμητικές τιμές για την θέση και την ταχύτητα ενός σώματος, μέσα στην εξέλιξη του χρόνου,όταν αυτό κινείται πάνω σε συγκεκριμένες τροχιές.Δεν συμβαίνει όμως το ίδιο σε ένα κβαντικό σύστημα, το οποίο περιγράφει η εξίσωση του Schrödinger, γιατί η τελευταία είναι μιγαδική:Στο αριστερό της μέρος υπάρχει το i (οπού i2=-1).Οι μιγαδικές λύσεις δεν μπορούν να αντιστοιχούν σε φυσικά μεγέθη του κλασικού κόσμου.Στον κβαντικό κόσμο,λοιπόν,δεν μας φανερώνουν παράδοξα γεγονότα μόνο τα πειράματα,άλλα και ο μαθηματικός φορμαλισμός θέτει ερμηνευτικά προβλήματα.Γιατί το ερώτημα τι είδους οντότητα είναι ένα σωματίδιο μεταξύ της αρχής και του τέλους της διαδρομής,στην λεγόμενη κβαντική κατάσταση,είναι ισοδύναμο με το τι περιγράφει η κυματοσυνάρτηση,ποιο είναι το υποκείμενο της ψ.Αν υποθέσουμε ότι έχουμε ένα τέτοιο κβαντικό σύστημα,π.χ. ένα ηλεκτρόνιο,το οποίο είναι απομονωμένο από το περιβάλλον του.Το σύστημα αυτό θα χαρακτηρίζεται από μια σειρά φυσικών μεγεθών,π.χ. ενέργεια,ταχύτητα, στροφορμή κ.τ.λ.Τα μεγέθη αυτά χαρακτηρίζουν την (αρχική) του κατάσταση. Όταν σε μια χρονική στιγμή ξέρουμε κάποια από αυτά τα μεγέθη,τότε με την βοήθεια της αντίστοιχης ψ μπορούμε να τα υπολογίσουμε σε μια επόμενη χρονική στιγμή και επομένως να γνωρίζουμε την κατάσταση του συστήματος μας.Για κάθε ένα από αυτά τα φυσικά μεγέθη υπάρχει ένας τελεστής,ο οποίος όταν εφαρμοσθεί στην ψ μας δίδει έναν κανόνα αντιστοίχισης για το συγκεκριμένο φυσικό μέγεθος.






.jpg)
.jpg)
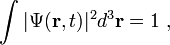


.jpg)

