ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΜΗΧΑΝΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ
ΥΔΡΟΣΤΑΤΙΚΗ ΠΙΕΣΗ
Υδροστατική πίεση ονομάζεται η πίεση που οφείλεται στο βάρος των υγρών.Η υδροστατική πίεση οφείλεται στη βαρύτητα.
Ένα απλό μανόμετρο είναι αυτό που βλέπουμε στο παρακάτω σχήμα.Μέσα στο λυγισμένο σωλήνα ρίχνουμε χρωματισμένο νερό η κάποιο άλλο υγρό,για παράδειγμα οινόπνευμα,υδράργυρο κ.λπ.
Γεμίζουμε έναν κύλινδρο με νερό και με τη βοήθεια του μανομέτρου μετράμε την πίεση σε διάφορα βάθη.
Παρατηρούμε ότι,όταν διπλασιάζεται το βάθος διπλασιάζεται και η πίεση,όταν τριπλασιάζεται το βάθος τριπλασιάζεται και η πίεση κ.ο.κ
α) του βάθους από την επιφάνεια του υγρού,
Θεωρούμε μέσα στο υγρό δύο σημεία Α και Β που βρίσκονται στο ίδιο οριζόντιο επίπεδο.Οι πιέσεις στα σημεία Α και Β δίνονται από του τύπους:
pA=ρ▪g▪h1 και
pΒ=ρ▪g▪h2
Επειδή το υγρό βρίσκεται σε ισορροπία,πρέπει οι πιέσεις σε όλα τα σημεία του,που βρίσκονται στο ίδιο οριζόντιο επίπεδο,να είναι ίσες.
Επομένως:
Η αρχή των συγκοινωνούντων δοχείων βρίσκει εφαρμογές στην κατασκευή των δεξαμενών ύδρευσης των πόλεων,στους πίδακες και συντριβάνια που στολίζουν τις πλατείες,στα αρτεσιανά πηγάδια κ.α.
Οι δεξαμενές κατασκευάζονται στα ψηλότερα σημεία έτσι ώστε το νερό να μπορεί να φθάσει και στους ψηλότερους ορόφους των σπιτιών χωρίς να χρειάζεται αντλία.
Η δεξαμενή του νερού και οι σωλήνες του δικτύου αποτελούν συγκοινωνούντα δοχεία.
Από την εποχή της αρχαίας Ρώμης,η έννοια των συγκοινωνούντων δοχείων έχει χρησιμοποιηθεί για την κατασκευή υδραγωγείων.
Στην παραπάνω εικόνα φαίνεται ένα Ρωμαϊκό υδραγωγείο.Το υδραγωγείο κατασκευάστηκε για να μεταφέρει νερό από την κορυφή Α σε μια πόλη σε χαμηλότερο υψόμετρο Β.
ΑΡΤΕΣΙΑΝΑ ΠΗΓΑΔΙΑ
Στους πίδακες και στα αρτεσιανά πηγάδια το νερό που πετιέται προς τα πάνω δε φτάνει ποτέ στο ύψος του νερού που βρίσκεται στο δοχείο η στη δεξαμενή,γιατί συναντάει στην κίνηση του διάφορες τριβές.
Στα αρτεσιανά πηγάδια το νερό αναβλύζει δημιουργώντας πίδακα.Τώρα θα μελετήσουμε το φαινόμενο αυτό.
Όταν η μορφολογία του υπεδάφους είναι κατάλληλη,μεταξύ δυο υδατοστεγών πετρωμάτων είναι δυνατόν να δημιουργηθεί μια υπόγεια δεξαμενή νερού,όπως φαίνεται στο παρακάτω σχήμα.
Ανοίγουμε στην περιοχή Κ ένα πηγάδι,που το βάθος του να φθάνει μέχρι την υπόγεια δεξαμενή.Τότε η δεξαμενή και το πηγάδι αποτελούν συγκοινωνούντα δοχεία.
Η ελεύθερη επιφάνεια του νερού και στα δυο πρέπει να βρίσκεται στο ίδιο οριζόντιο επίπεδο.Σύμφωνα με την αρχή των συγκοινωνούντων δοχείων,το νερό αναπηδά στο πηγάδι για να φθάσει στην ελεύθερη επιφάνεια ΑΑ΄.
Με αυτό τον τρόπο σχηματίζεται ένας πίδακας.Βέβαια,λόγω τριβών με τον ατμοσφαιρικό αέρα,ο πίδακας δε φθάνει μέχρι το ύψος της επιφάνειας ΑΑ΄.
ΑΤΜΟΣΦΑΙΡΙΚΗ ΠΙΕΣΗ
Η ατμοσφαιρική πίεση μετρήθηκε για πρώτη φορά το 1643 από το μαθητή του Γαλιλαίου,τον Ιταλό μαθηματικό και φυσικό Εβαγγελίστα Τορικέλι.Ο Τορικέλι για να μετρήσει την ατμοσφαιρική πίεση έκανε ένα πείραμα,που έγινε γνωστό ως πείραμα του Τορικέλι.
Το πείραμα αυτό αποτελείται μία ακόμη απόδειξη για την ύπαρξη ατμοσφαιρικής πίεσης.Ο γύρω αέρας πιέζει την επιφάνεια του υδραργύρου της λεκάνης και συγκρατεί τον υδράργυρο μέσα στο σωλήνα σε κάποιο ύψος h.Αν το πείραμα γίνεται στην επιφάνεια της θάλασσας το ύψος h βρίσκεται ότι είναι 76 cm.
Το υγρό μέσα στο σωλήνα και τη λεκάνη ισορροπεί, άρα σύμφωνα με την αρχή των συγκοινωνούντων δοχείων θα ισχύει:
 |
| ΦΥΣΙΚΗ Γ ΛΥΚΕΙΟΥ ΜΗΧΑΝΙΚΗ ΤΩΝ ΡΕΥΣΤΩΝ |
ΕΙΣΑΓΩΓΗ
Ένα υγρό που βρίσκεται μέσα σε δοχείο λόγω του βάρους του πιέζει τον πυθμένα του δοχείου.Αφού το υγρό ισορροπεί,η δύναμη που ασκεί στον πυθμένα του δοχείου ισούται με το βάρος του.
Άρα από τον ορισμό της πίεσης μπορούμε να πούμε ότι είναι ίση με το πηλίκο του βάρους του υγρού προς το εμβαδόν του πυθμένα.
Αν είχαμε τη δυνατότητα να μεταφέρουμε ένα κλειστό δοχείο γεμάτο με νερό από την επιφάνεια της γης στην επιφάνεια της σελήνης, θα διαπιστώναμε ότι η υδροστατική πίεση στον πυθμένα του έχει τιμή περίπου 6 φορές μικρότερη από την τιμή της στην επιφάνεια της γης.Αυτό συμβαίνει γιατί το βάρος του νερού στη σελήνη είναι 6 φορές μικρότερο από το βάρος του στη γη.
ΟΡΙΣΜΟΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΠΙΕΣΗΣ
Ένα υγρό που βρίσκεται μέσα σε δοχείο λόγω του βάρους του πιέζει τον πυθμένα του δοχείου.Αφού το υγρό ισορροπεί,η δύναμη που ασκεί στον πυθμένα του δοχείου ισούται με το βάρος του.
Άρα από τον ορισμό της πίεσης μπορούμε να πούμε ότι είναι ίση με το πηλίκο του βάρους του υγρού προς το εμβαδόν του πυθμένα.
.jpg) |
Ένα υγρό που βρίσκεται μέσα σε δοχείο λόγω του βάρους του πιέζει τον πυθμένα του δοχείου.Αφού το υγρό ισορροπεί, η δύναμη που ασκεί στον πυθμένα του δοχείου ισούται με το βάρος του |
ΟΡΙΣΜΟΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΠΙΕΣΗΣ
Θεωρούμε ένα δοχείο με νερό.Το νερό,σύμφωνα με τα προηγούμενα, δημιουργεί πίεση στα τοιχώματα του δοχείου,γι' αυτό τινάζεται από τις τρύπες κάποια στιγμή.
Είναι φανερό ότι η πίεση στο δοχείο οφείλεται στο βάρος W του νερού.
.JPG) |
| Το νερό δημιουργεί πίεση στα τοιχώματα του δοχείου,γι' αυτό τινάζεται από τις τρύπες κάποια στιγμή |
.jpg) |
| Υδροστατική πίεση ονομάζεται η πίεση που οφείλεται στο βάρος των υγρών |
ΜΕΤΡΗΣΗ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΠΙΕΣΗΣ
Μανόμετρα ονομάζονται τα όργανα με τα οποία μετράμε την πίεση σε κάποιο σημείο ενός υγρού η αερίου.
Με το μανόμετρο μετράμε την πίεση που ασκείται στην επιφάνεια μιας ελαστικής μεμβράνης, την οποία βυθίζουμε μέσα στο υγρό.Ο σωλήνας τύπου U περιέχει υδράργυρο ή κάποιο άλλο υγρό, συνήθως λάδι. Η διαφορά ύψους του υγρού στα δύο σκέλη του σωλήνα είναι ανάλογη της υδροστατικής πίεσης.
.JPG) |
| Μανόμετρα ονομάζονται τα όργανα με τα οποία μετράμε την πίεση σε κάποιο σημείο ενός υγρού ή αερίου |
.JPG) |
| Απλό ανοιχτό μανόμετρο.Μέσα στο λυγισμένο σωλήνα ρίχνουμε χρωματισμένο νερό |
Αν δημιουργήσουμε πίεση στο ένα σκέλος του σωλήνα,π.χ. φυσώντας αέρα,παρατηρούμε ότι το υγρό κατεβαίνει στο σκέλος Α και ανεβαίνει στο Β.Έτσι,δημιουργείται μία διαφορά ύψους z του υγρού στα δύο σκέλη του σωλήνα.Αν αυξήσουμε την πίεση στο σκέλος Α,παρατηρούμε ότι αυξάνει και η διαφορά ύψους z.Άρα η διαφορά στάθμης του υγρού στο σωλήνα αποτελεί ένα μέτρο για την πίεση που επικρατεί στο σκέλος Α.Έτσι ο λυγισμένος σωλήνας με το υγρό μπορεί να χρησιμοποιηθεί ως μανόμετρο.
Όταν θέλουμε να μετρήσουμε την πίεση ενός αερίου,που είναι κλεισμένο σε φιάλη συνδέουμε τον ελαστικό σωλήνα με τη φιάλη,όπως συνδέσαμε τους πνεύμονες μας.
Όταν,όμως θέλουμε να μετρήσουμε την πίεση σε κάποιο σημείο υγρού,χρησιμοποιούμε μία μανομετρική κάψα.
.JPG) |
| Ανοιχτό μανόμετρο και μία μανομετρική κάψα .Η μανομετρική κάψα είναι ένα μικρό δοχείο,που έχει στο στόμιό του μία λεπτή,ελαστική μεμβράνα |
Η μανομετρική κάψα είναι ένα μικρό δοχείο(μεταλλικό ή γυάλινο),που έχει στο στόμιό του μία λεπτή,ελαστική μεμβράνα.Αν πιέσουμε τη μεμβράνα,πιέζεται ο αέρας που υπάρχει στην κάψα και η πίεση αυτή φτάνει στο μανόμετρο μέσα από τον ελαστικό σωλήνα
ΝΟΜΟΣ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ
Η υδροστατική πίεση οφείλεται στη βαρύτητα.Τώρα θα προσπαθήσουμε να βρούμε τις σχέσεις που σχετίζεται η υδροστατική πίεση.Για να το καταφέρουμε αυτό θα πρέπει να καταφύγουμε στην πειραματική μέτρηση.
ΥΔΡΟΣΤΑΤΙΚΗ ΠΙΕΣΗ ΚΑΙ ΠΡΟΣΑΝΑΤΟΛΙΣΜΟΣ
Βυθίζουμε τη μανομετρική κάψα σε δοχείο με νερό και σημειώνουμε τη διαφορά ύψους h στα δύο σκέλη του μανομέτρου.Κατόπιν γυρίζουμε την κάψα,ώστε να αλλάξει προσανατολισμό η μεμβράνα της και παρατηρούμε ότι δε μεταβάλλεται η ένδειξη του μανομέτρου.
.JPG) |
| Η επιφάνεια βρίσκεται σε βάθος h και είναι οριζόντια |
Στη συνέχεια μετατοπίζουμε την κάψα μέσα στο νερό,με τρόπο ώστε το κέντρο της να παραμείνει στο ίδιο βάθος και παρατηρούμε ότι πάλι δεν αλλάζει η πίεση.
Άρα:
.JPG) |
Η επιφάνεια βρίσκεται σε βάθος h και είναι κατακόρυφη
|
Η πίεση,που προκαλεί ένα υγρό σε μία επιφάνεια,δεν εξαρτάται από τον προσανατολισμό της επιφάνειας,αλλά είναι ίδια σε όλα τα σημεία του υγρού που βρίσκονται στο ίδιο οριζόντιο επίπεδο.
Από το πείραμα αυτό καταλαβαίνουμε ότι η υδροστατική πίεση είναι μονόμετρο μέγεθος.
ΥΔΡΟΣΤΑΤΙΚΗ ΠΙΕΣΗ ΚΑΙ ΒΑΘΟΣ
Όταν κολυμπάμε στην πισίνα του κολυμβητηρίου ή στην θάλασσα διαπιστώνουμε ότι όσο πιο βαθιά βουτάμε,τόσο μεγαλύτερη πίεση αισθανόμαστε στ' αυτιά μας.
Για να εξηγήσουμε αυτό το φαινόμενο θα εκτελέσουμε το παρακάτω πείραμα.
.JPG) |
| Όταν κολυμπάμε στην θάλασσα διαπιστώνουμε ότι όσο πιο βαθιά βουτάμε,τόσο μεγαλύτερη πίεση αισθανόμαστε στ' αυτιά μας |
.JPG) |
| Η υδροστατική πίεση είναι ανάλογη προς το βάθος |
.JPG) |
| Σε διπλάσιο βάθος έχουμε διπλάσια υδροστατική πίεση |
Πρέπει να σημειώσουμε ότι η πίεση,που μετράει το μανόμετρο που χρησιμοποιούμε και η οποία μας ενδιαφέρει στην ενότητα αυτή,είναι η υδροστατική πίεση,δηλαδή η πίεση που προέρχεται από το βάρος του υγρού που βρίσκεται κάθε φορά πάνω από τη μανομετρική κάψα.
Άρα:
.JPG) |
| H υδροστατική πίεση αυξάνεται με το βάθος |
Η υδροστατική πίεση είναι ανάλογη προς το βάθος.
ΥΔΡΟΣΤΑΤΙΚΗ ΠΙΕΣΗ ΚΑΙ ΕΙΔΟΣ ΥΓΡΟΥ
Βάζουμε σε ένα δοχείο καθαρό νερό και σε ένα άλλο δοχείο πυκνό αλατόνερο.Κατόπιν βυθίζουμε τη μανομετρική κάψα στο ίδιο βάθος και στα δύο δοχεία και σημειώνουμε τις ενδείξεις του μανομέτρου.
Παρατηρούμε ότι η πίεση στο καθαρό νερό είναι μικρότερη από την πίεση στο αλατόνερο,αν και το βάθος είναι το ίδιο.
.JPG) |
| Το αλατόνερο έχει μεγαλύτερη πυκνότητα από το καθαρό νερό |
Αν λάβουμε υπόψη μας ότι το αλατόνερο έχει μεγαλύτερη πυκνότητα από το καθαρό νερό,συμπεραίνουμε ότι η υδροστατική πίεση αυξάνεται με την πυκνότητα του υγρού.Με προσεκτικά πειράματα αποδεικνύεται ότι:
Η υδροστατική πίεση είναι ανάλογη της πυκνότητας του υγρού.
ΝΟΜΟΣ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ
ΝΟΜΟΣ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ
Συγκεντρώνοντας τα προηγούμενα συμπεράσματα,μπορούμε να πούμε ότι η υδροστατική πίεση είναι ανάλογη:
.jpg) |
| Η υδροστατική πίεση είναι ανάλογη του βάθους από την επιφάνεια του υγρού,της πυκνότητας του υγρού και της επιτάχυνσης της βαρύτητας |
β) της πυκνότητας του υγρού,
γ) της επιτάχυνσης της βαρύτητας.
Υδροστατική πίεση=πυκνότητα υγρού× επιτάχυνση της βαρύτητας× βάθος από την επιφάνεια του υγρού
p=ρ▪g▪h
νόμος της υδροστατικής πίεσης
όπου:
p η υδροστατική πίεση που τη μετράμε σε Ν/m2
ρ η πυκνότητα του υγρού που τη μετράμε σε kgr/m3
g η επιτάχυνση της βαρύτητας που τη μετράμε σε m/sec2 και
Πρέπει να τονίσουμε ότι η υδροστατική πίεση δεν εξαρτάται από το σχήμα του δοχείου,τον όγκο του υγρού και την συνολική μάζα του νερού.
Στα σημεία Α και Β που φαίνονται στην παραπάνω εικόνα η πίεση του νερού είναι ίδια, διότι βρίσκονται στο ίδιο βάθος, παρότι ο όγκος του νερού στην αβαθή λίμνη είναι πολύ μεγαλύτερος απ' ότι στη βαθιά λίμνη.
Αισθανόμαστε την ίδια πίεση όταν κάνουμε μια βουτιά και το κεφάλι μας βυθιστεί κατά ένα μέτρο είτε σε μια μικρή πισίνα με θαλασσινό νερό, είτε στη μέση του πελάγους.
Στα σημεία Α και Β που φαίνονται στην παραπάνω εικόνα η πίεση του νερού είναι ίδια, διότι βρίσκονται στο ίδιο βάθος, παρότι ο όγκος του νερού στην αβαθή λίμνη είναι πολύ μεγαλύτερος απ' ότι στη βαθιά λίμνη.
.jpg) |
| Κατά την διάρκεια της κατάδυσης ο όγκος των πνευμόνων μειώθηκε λόγω της συμπίεσης του θώρακος με αποτέλεσμα αυξημένη μερική πίεση Ο2 , CO2, και Ν στους πνεύμονες |
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΠΙΕΣΗΣ
ΣΥΓΚΟΙΝΩΝΟΥΝΤΑ ΔΟΧΕΙΑ
ΕΙΣΑΓΩΓΗ
Χρησιμοποιούμε τη συσκευή του παρακάτω σχήματος η οποία αποτελείται από διάφορα δοχεία που συγκοινωνούν μεταξύ τους.Ρίχνουμε νερό στη συσκευή και το αφήνουμε να ισορροπήσει.Παρατηρούμε ότι η ελεύθερη επιφάνεια του νερού φτάνει στο ίδιο οριζόντιο επίπεδο σε όλα τα δοχεία.Το ίδιο συμβαίνει και για κάθε άλλο υγρό.
Το υγρό που βρίσκεται στον κοινό οριζόντιο σωλήνα ισορροπεί.Για να συμβαίνει αυτό, θα πρέπει σε όλα τα σημεία του να επικρατεί η ίδια πίεση. Αν σε κάποιο σημείο η πίεση ήταν διαφορετική, τότε θα ασκούνταν επιπλέον δύναμη που θα προκαλούσε την κίνηση του υγρού.
.jpg) |
| Το υγρό που βρίσκεται στον κοινό οριζόντιο σωλήνα ισορροπεί.Για να συμβαίνει αυτό, θα πρέπει σε όλα τα σημεία του να επικρατεί η ίδια πίεση |
Από το νόμο της υδροστατικής προκύπτει ότι αν σε κάποιο από τα δοχεία η στάθμη του υγρού ήταν σε μεγαλύτερο ύψος, η πίεση στο αντίστοιχο σημείο του κοινού σωλήνα θα ήταν μεγαλύτερη.
ΑΡΧΗ ΤΩΝ ΣΥΓΚΟΙΝΟΝΟΥΝΤΩΝ ΔΟΧΕΙΩΝ
Άρα από το παραπάνω πείραμα μπορούμε να συμπαιράνουμε ότι:
Όταν μέσα σε συγκοινωνούντα δοχεία ισορροπεί ένα υγρό,όλα τα σημεία του υγρού έχουν την ίδια πίεση και η ελεύθερη επιφάνεια του σε όλα τα δοχεία βρίσκεται στο ίδιο οριζόντιο επίπεδο.
Το συμπέρασμα αυτό είναι γνωστό σαν αρχή των συγκοινονούντων δοχείων.
Αυτό συμβαίνει ακόμη και όταν το υγρό βρίσκεται σε διαφορετικά, αλλά συγκοινωνούντα δοχεία.
Σε αντίθετη περίπτωση που τα υγρά είναι διαφορετικής πυκνότητας, η επιφάνεια του πιο πυκνού είναι χαμηλότερη από το αραιότερο.
Ο λόγος των αποστάσεων της επιφάνειας είναι αντίστροφος προς το λόγο της πυκνότητας των δυο υγρών.
Ο ΝΟΜΟΣ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΣΤΑ ΣΥΓΚΟΙΝΟΝΟΥΝΤΑ ΔΟΧΕΙΑ
Η παραπάνω αρχή μπορεί να προκύψει θεωρητικά από το βασικό νόμο της υδροστατικής.
.jpg) |
| Τέσσερεις κάθετα τοποθετημένοι γυάλινοι σωλήνες συνδεδεμένοι μεταξύ τους για την απόδειξη ότι η στάθμη του νερού είναι στο ίδιο ύψος και ανεξάρτητη του σχήματος του σωλήνα |
 |
| Στην περίπτωση που τα υγρά είναι διαφορετικής πυκνότητας,η επιφάνεια του πιο πυκνού είναι χαμηλότερη από το αραιότερο |
.jpg) |
| Ο λόγος των αποστάσεων της επιφάνειας είναι αντίστροφος προς το λόγο της πυκνότητας των δυο υγρών |
Ο ΝΟΜΟΣ ΤΗΣ ΥΔΡΟΣΤΑΤΙΚΗΣ ΣΤΑ ΣΥΓΚΟΙΝΟΝΟΥΝΤΑ ΔΟΧΕΙΑ
Η παραπάνω αρχή μπορεί να προκύψει θεωρητικά από το βασικό νόμο της υδροστατικής.
 |
| To νερό ρέει από την υψηλότερη προς την χαμηλότερη επιφάνεια μέχρι που να βρίσκονται στο ίδιο οριζόντιο επίπεδο |
pA=ρ▪g▪h1 και
pΒ=ρ▪g▪h2
Επειδή το υγρό βρίσκεται σε ισορροπία,πρέπει οι πιέσεις σε όλα τα σημεία του,που βρίσκονται στο ίδιο οριζόντιο επίπεδο,να είναι ίσες.
Επομένως:
pA=pΒ ή
ρ▪g▪h1=ρ▪g▪h2 ή
h1=h2
ρ▪g▪h1=ρ▪g▪h2 ή
h1=h2
Άρα οι επιφάνειες του υγρού στα διάφορα δοχεία πρέπει να βρίσκονται στο ίδιο οριζόντιο επίπεδο.
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΑΡΧΗΣ ΤΩΝ ΣΥΓΚΟΙΝΩΝΟΥΝΤΩΝ ΔΟΧΕΙΩΝ
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΑΡΧΗΣ ΤΩΝ ΣΥΓΚΟΙΝΩΝΟΥΝΤΩΝ ΔΟΧΕΙΩΝ
.JPG) |
| Η αρχή των συγκοινωνούντων δοχείων βρίσκει εφαρμογές στα συντριβάνια |
.jpg) |
| Οι δεξαμενές κατασκευάζονται στα ψηλότερα σημεία |
.jpg) |
| Η δεξαμενή του νερού και οι σωλήνες του δικτύου αποτελούν συγκοινωνούντα δοχεία |
.jpg) |
| Ένα Ρωμαϊκό υδραγωγείο.Το υδραγωγείο κατασκευάστηκε για να μεταφέρει νερό από την κορυφή Α σε μια πόλη σε χαμηλότερο υψόμετρο Β |
ΑΡΤΕΣΙΑΝΑ ΠΗΓΑΔΙΑ
Τα αρτεσιανά πηγάδια είναι βαθιά ορύγματα στο έδαφος,από τα οποία αναβλύζει το νερό,με τη μορφή μικρού πίδακα.
Για να συμβαίνει αυτή η φυσική αναπήδηση του νερού πρέπει το υδροφόρο στρώμα να βρίσκεται ανάμεσα σε υδατοστεγή(αργιλικά) στρώματα και η στάθμη του νερού στο υδροφόρο στρώμα να βρίσκεται πάνω από το στόμιο του πηγαδιού.
.jpg) |
| Ένα αρτεσιανό πηγάδι |
.gif) |
| Τα αρτεσιανά πηγάδια είναι βαθιά ορύγματα στο έδαφος,από τα οποία αναβλύζει το νερό,με τη μορφή μικρού πίδακα |
.JPG) |
| Στα αρτεσιανά πηγάδια το νερό που πετιέται προς τα πάνω δε φτάνει ποτέ στο ύψος του νερού που βρίσκεται στο δοχείο η στη δεξαμενή,γιατί συναντάει στην κίνηση του διάφορες τριβές |
.jpg) |
| Στα αρτεσιανά πηγάδια το νερό αναβλύζει δημιουργώντας πίδακα |
.jpg) |
| Ανοίγουμε στην περιοχή Κ ένα πηγάδι, που το βάθος του να φθάνει μέχρι την υπόγεια δεξαμενή.Τότε η δεξαμενή και το πηγάδι αποτελούν συγκοινωνούντα δοχεία |
.jpg) |
| Η δεξαμενή και το πηγάδι αποτελούν συγκοινωνούντα δοχεία |
.jpg) |
| Σύμφωνα με την αρχή των συγκοινωνούντων δοχείων, το νερό αναπηδά στο πηγάδι για να φθάσει στην ελεύθερη επιφάνεια |
ΤΟ ΠΕΙΡΑΜΑ ΤΟΥ ΤΟΡΙΚΕΛΙ
ΕΙΣΑΓΩΓΗ
Είναι γνωστό ότι η γη περιβάλλεται από ένα στρώμα αέρα που λέγεται ατμόσφαιρα.Η ατμόσφαιρα αποτελείται από ένα μείγμα αερίων που ονομάζεται ατμοσφαιρικός αέρας.
.JPG) |
| Ατμόσφαιρα ονομάζεται ένα λεπτό στρώμα αερίων που περιβάλλει περιβάλλει τη Γη |
Ατμόσφαιρα ονομάζεται ένα λεπτό στρώμα αερίων που περιβάλλει περιβάλλει τη Γη.Εάν η Γη είχε μέγεθος μπάλας μπάσκετ, η ατμόσφαιρα θα είχε πάχος ενός φύλλου χαρτιού.
Η σύνθεση της ατμόσφαιρας είναι:
Άζωτο (78%),
Οξυγόνο (21%),
Άλλα αέρια (1%)
Ο αέρας είναι διαφανής.Έχει μάζα και από τη γη ασκείται σε αυτόν η δύναμη του βάρους. Επομένως, όπως συμβαίνει με όλα τα ρευστά σώματα, ασκεί πίεση σε κάθε επιφάνεια που βρίσκεται μέσα σ' αυτόν.Όπως ακριβώς η υδροστατική πίεση μιας κατακόρυφης στήλης νερού οφείλεται στο βάρος της, έτσι και η ατμοσφαιρική πίεση οφείλεται στο βάρος του αέρα.
.jpg) |
| Η σύνθεση της ατμόσφαιρας |
Ο αέρας,όπως και κάθε άλλο σώμα,έλκεται από τη γη,και η έλξη αυτή συγκρατεί τα μόρια του και δεν τα αφήνει να φύγουν προς το διάστημα.Εξαιτίας της γήινης έλξεως ο αέρας έχει βάρος,το οποίο προκαλεί πίεση στην επιφάνεια της γης,αλλά και σε κάθε άλλη επιφάνεια που βρίσκεται σε επαφή με τον αέρα.Η πίεση αυτή ονομάζεται ατμοσφαιρική πίεση.
Ατμοσφαιρική πίεση ονομάζεται η πίεση που δημιουργείται από την ατμόσφαιρα.
Η τιμή της ατμοσφαιρικής πίεσης εξαρτάται από το ύψος από την επιφάνεια της θάλασσας.Όσο μεγαλύτερο είναι το υψόμετρο στο οποίο βρισκόμαστε τόσο μικρότερη είναι η ατμοσφαιρική πίεση γιατί είναι λιγότερη η ποσότητα του αέρα που βρίσκεται πάνω από εμάς και μας πιέζει με το βάρος της.
Τα ανώτερα στρώματα της ατμόσφαιρας πιέζουν, λόγω του βάρους τους, τα κατώτερα με αποτέλεσμα η τιμή της πίεσης να είναι μεγαλύτερη στην επιφάνεια της θάλασσας.Αντιλαμβανόμαστε την ατμοσφαιρική πίεση μόνο όταν υπάρχει διαφορά πίεσης.
Πίεση μιας ατμόσφαιρας (1 atm) ονομάζεται τιμή της ατμοσφαιρικής πίεσης στην επιφάνεια της θάλασσας.
Η τιμή αυτή σημαίνει ότι σε κάθε τετραγωνικό μέτρο επιφάνειας ασκείται δύναμη 100000Ν!Η επιφάνεια του σώματος μας είναι περίπου ένα με δύο τετραγωνικά μέτρα και άρα και το σώμα μας δέχεται από τον ατμοσφαιρικό αέρα μια τόσο μεγάλη δύναμη η οποία κανονικά έπρεπε να μας συνθλίψει.Το σώμα μας όμως είναι φτιαγμένο ώστε να έχει την ίδια πίεση στο εσωτερικό του και έτσι να αντισταθμίζεται και να εξουδετερώνεται η επίδραση της ατμοσφαιρικής πίεσης που ασκείται εξωτερικά.
Η τιμή της ατμοσφαιρικής πίεσης εξαρτάται από το ύψος από την επιφάνεια της θάλασσας.Όσο μεγαλύτερο είναι το υψόμετρο στο οποίο βρισκόμαστε τόσο μικρότερη είναι η ατμοσφαιρική πίεση γιατί είναι λιγότερη η ποσότητα του αέρα που βρίσκεται πάνω από εμάς και μας πιέζει με το βάρος της.
.JPG) |
| Η τιμή της ατμοσφαιρικής πίεσης εξαρτάται από το ύψος από την επιφάνεια της θάλασσας.Όσο μεγαλύτερο είναι το υψόμετρο στο οποίο βρισκόμαστε τόσο μικρότερη είναι η ατμοσφαιρική πίεση |
.JPG) |
| Πίεση μιας ατμόσφαιρας (1 atm) ονομάζεται τιμή της ατμοσφαιρικής πίεσης στην επιφάνεια της θάλασσας |
Η τιμή αυτή σημαίνει ότι σε κάθε τετραγωνικό μέτρο επιφάνειας ασκείται δύναμη 100000Ν!Η επιφάνεια του σώματος μας είναι περίπου ένα με δύο τετραγωνικά μέτρα και άρα και το σώμα μας δέχεται από τον ατμοσφαιρικό αέρα μια τόσο μεγάλη δύναμη η οποία κανονικά έπρεπε να μας συνθλίψει.Το σώμα μας όμως είναι φτιαγμένο ώστε να έχει την ίδια πίεση στο εσωτερικό του και έτσι να αντισταθμίζεται και να εξουδετερώνεται η επίδραση της ατμοσφαιρικής πίεσης που ασκείται εξωτερικά.
ΕΞΗΓΗΣΗ ΤΗΣ ΑΤΜΟΣΦΑΙΡΙΚΗΣ ΠΙΕΣΗΣ
Ένα απλό πείραμα που αποδεικνύει την ύπαρξη της ατμοσφαιρικής πίεσης είναι αυτό με τον ελαστικό δίσκο,την γνωστή μας βεντούζα.Αν εφαρμόσουμε τον ελαστικό δίσκο σε κάποια λεία επιφάνεια,για παράδειγμα στο τζάμι,και επιχειρήσουμε να τον αποκολλήσουμε τραβώντας τον άγκιστρο,θα συναντήσουμε μεγάλη δυσκολία.Αν όμως ανασηκώσουμε λίγο τα χείλη του,ώστε να περάσει αέρας ανάμεσα στο δίσκο και στο τζάμι,η αποκόλληση γίνεται χωρίς προσπάθεια.
Το φαινόμενο εξηγείται ως εξής:
.JPG) |
| Η βεντούζα με άγκιστρο |
Όταν δεν υπάρχει αέρας ανάμεσα στο δίσκο και το τζάμι,ο δίσκος πιέζεται μόνο από την έξω επιφάνεια του και κολλάει στο τζάμι.Όταν όμως μπαίνει αέρας ανάμεσα στο δίσκο και το τζάμι,αναπτύσσεται πιεστική δύναμη και στη μέσα επιφάνεια του δίσκου και ο δίσκος αποχωρίζεται εύκολα.
Ένα άλλο πείραμα που φανερώνει την ύπαρξη της ατμοσφαιρικής πιέσεως είναι και το ακόλουθο.
.JPG) |
| Προσαρμόζουμε μία ελαστική μεμβράνη στο μεγάλο στόμιο ενός χωνιού και μετά ρουφάμε τον αέρα από το χωνί |
Προσαρμόζουμε μία ελαστική μεμβράνη στο μεγάλο στόμιο ενός χωνιού και μετά ρουφάμε τον αέρα από το χωνί.Το γεγονός αυτό φανερώνει ότι κάποια δύναμη ενεργεί πάνω στην εξωτερική επιφάνεια της μεμβράνης και τη σπρώχνει προς τα μέσα.Φυσικά η δύναμη αυτή δεν εμφανίζεται τη στιγμή που αφαιρούμε τον αέρα από το χωνί,αλλά υπάρχει από πριν,αν και δε γίνεται αντιληπτοί στην αρχή,γιατί η επιφάνεια πιέζεται εξίσου και από τις δύο όψεις (F'=F).
Αφαιρώντας τον αέρα μικραίνει η εσωτερική πίεση,άρα και η πιεστική δύναμη F',καταστρέφεται η ισορροπία και η μεμβράνα ωθείται προς τα μέσα,ώσπου βρίσκει άλλη θέση ισορροπίας.
ΜΕΤΡΗΣΗ ΤΗΣ ΑΤΜΟΣΦΑΙΡΙΚΗΣ ΠΙΕΣΗΣ
Η ατμοσφαιρική πίεση μετρήθηκε για πρώτη φορά το 1643 από το μαθητή του Γαλιλαίου,τον Ιταλό μαθηματικό και φυσικό Εβαγγελίστα Τορικέλι.Ο Τορικέλι για να μετρήσει την ατμοσφαιρική πίεση έκανε ένα πείραμα,που έγινε γνωστό ως πείραμα του Τορικέλι.
.JPG) |
| Ο Ιταλός μαθηματικός και φυσικός Εβαγγελίστα Τορικέλι (1608 - 1647) |
Γεμίζουμε με υδράργυρο ένα γυάλινο σωλήνα που έχει μήκος 1 m περίπου,κλείνουμε το στόμιο του με το δάκτυλό μας και το αναποδογυρίζουμε σε μία μικρή λεκάνη με υδράργυρο,φροντίζοντας να φέρουμε το στόμιο του κάτω από την επιφάνεια του υδραργύρου.
.JPG) |
| Γεμίζουμε με υδράργυρο ένα γυάλινο σωλήνα που έχει μήκος 1 m περίπου,κλείνουμε το στόμιο του με το δάκτυλό μας και το αναποδογυρίζουμε σε μία μικρή λεκάνη με υδράργυρο |
Μετά αποσύρουμε το δάκτυλό μας και παρατηρούμε ότι ο υδράργυρος κατεβαίνει και σταθεροποιείται σε ορισμένη στάθμη που βρίσκεται σε ύψος h πάνω από την επιφάνεια του υδραργύρου της λεκάνης.Γέρνουμε λίγο το σωλήνα και παρατηρούμε ότι η στάθμη παραμένει διαρκώς στο ίδιο ύψος h.
| Γέρνουμε λίγο το σωλήνα και παρατηρούμε ότι η στάθμη παραμένει διαρκώς στο ίδιο ύψος h |
 |
| Το πείραμα του Τορικέλι |
PA=PΒ
διότι τα Β, Α είναι σημεία του ίδιου υγρού και βρίσκονται στο ίδιο οριζόντιο επίπεδο. Η πίεση στο Α ισούται με την ατμοσφαιρική πίεση:
PA=Patm
Επομένως, η στήλη του υδραργύρου συγκρατείται από τη δύναμη που ασκείται, λόγω της ατμοσφαιρικής πίεσης, στην ελεύθερη επιφάνεια του υδραργύρου της λεκάνης. Μέσα στο σωλήνα πάνω από τη στήλη του υδραργύρου δημιουργήθηκε κενό.
Η πίεση στην επιφάνεια της στήλης είναι ίση με το μηδέν και συνεπώς η πίεση στο Β ισούται με την υδροστατική πίεση της στήλης του υδραργύρου:
.JPG) |
| Η πίεση στο Α είναι ίση με την πίεση στο Β |
ΡΒ=Ρυδρ
Συγκρίνουμε τις τελευταίες σχέσεις και συμπεραίνουμε ότι η ατμοσφαιρική πίεση είναι ίση με την πίεση που ασκεί στη βάση της στήλη υδραργύρου ύψους h.Σύμφωνα με την ισορροπία δυνάμεων όπου η συνολική δύναμη που δέχεται ο υδράργυρος από την ατμόσφαιρα ισούται με το βάρος του υδραργύρου που βρίσκεται πάνω από την επιφάνεια του υδραργύρου την λεκάνη στον δοκιμαστικό σωλήνα. Έτσι, απέδειξε ότι υπάρχει ατμοσφαιρική πίεση.Όταν h=76 cm ή 760 mm, λέμε ότι η ατμοσφαιρική πίεση ισούται με 760 mmHg.
Την υδροστατική πίεση που ασκεί στήλη υδραργύρου ύψους 1mm την ονομάζουμε 1 Torr προς τιμή του Τορικέλι. Επομένως μπορούμε να πούμε ότι η ατμοσφαιρική πίεση είναι 760 Torr.
Την υδροστατική πίεση που ασκεί στήλη υδραργύρου ύψους 1mm την ονομάζουμε 1 Torr προς τιμή του Τορικέλι. Επομένως μπορούμε να πούμε ότι η ατμοσφαιρική πίεση είναι 760 Torr.
.JPG) |
| Τη στήλη υδραργύρου ύψους 1mm την ονομάζουμε 1 Torr προς τιμή του Τορικέλι |
Με το πείραμα του ο Τορικέλι όχι μόνο απέδειξε την ύπαρξη της ατμοσφαιρικής πίεσης αλλά και την υπολόγισε κιόλας.Σημειώνουμε εδώ ότι στο χώρο πάνω από την επιφάνεια του υδραργύρου μέσα στο σωλήνα δεν υπάρχει αέρας, ο χώρος είναι κενός και επομένως η πίεση στο χώρο αυτό είναι μηδενική.
.JPG) |
| Βαρόμετρο είναι ειδικό όργανο μέτρησης της ατμοσφαιρικής πίεσης |
Τα όργανα που χρησιμοποιούνται για τη μέτρηση της ατμοσφαιρικής πίεσης ονομάζονται βαρόμετρα.Το πρώτο βαρόμετρο κατασκευάστηκε από τον Τορικέλι.
Βαρόμετρο είναι ειδικό όργανο μέτρησης της ατμοσφαιρικής πίεσης.
Η μετάδοση των πιέσεων μέσα στη μάζα των υγρών βρίσκει εφαρμογές στη λειτουργία του υδραυλικού πιεστηρίου,του υδραυλικού γερανού,του υδραυλικού φρένου,του υδραυλικού ανυψωτήρα κ.α.
Βαρόμετρο είναι ειδικό όργανο μέτρησης της ατμοσφαιρικής πίεσης.
ΜΕΤΑΔΟΣΗ ΤΩΝ ΠΙΕΣΕΩΝ ΣΤΑ ΡΕΥΣΤΑ ΑΡΧΗ ΤΟΥ ΠΑΣΚΑΛ
.jpg) |
| ΜΕΤΑΔΟΣΗ ΤΩΝ ΠΙΕΣΕΩΝ ΣΤΑ ΡΕΥΣΤΑ ΑΡΧΗ ΤΟΥ ΠΑΣΚΑΛ |
ΕΙΣΑΓΩΓΗ
Για να αντικαταστήσουμε το σκασμένο λάστιχο ενός αυτοκινήτου,πρέπει να το ανυψώσουμε.
Έχουμε παρατηρήσει ότι για το κάνουμε χρησιμοποιούμε κατάλληλες αντλίες.Θα μελετήσουμε αναλυτικά που στηρίζεται η λειτουργία μιας τέτοιας αντλίας.
Για να αντικαταστήσουμε το σκασμένο λάστιχο ενός αυτοκινήτου,πρέπει να το ανυψώσουμε.
.jpg) |
| Για να αντικαταστήσουμε το σκασμένο λάστιχο ενός αυτοκινήτου,πρέπει να το ανυψώσουμε.Έχουμε παρατηρήσει ότι για το κάνουμε χρησιμοποιούμε κατάλληλες αντλίες |
ΑΡΧΗ ΤΟΥ ΠΑΣΚΑΛ
Σε μία φιάλη τοποθετούμε χρωματισμένο υγρό(π.χ.νερό) και κλείνουμε τη φιάλη με ένα πώμα μέσα από το οποίο έχουμε περάσει μερικούς σωλήνες.Σημειώνουμε το ύψος του νερού που βρίσκεται στους σωλήνες προτού πιέσουμε την ελαστική σφαίρα Σ.Μετά πιέζουμε τη σφαίρα και παρατηρούμε ότι και στους τρεις σωλήνες το χρωματισμένο υγρό ανέρχεται κατά το ίδιο ύψος h.Αυτό σημαίνει ότι η πίεση,που δημιουργήθηκε στην ελεύθερη επιφάνεια του υγρού,μεταδόθηκε η ίδια σε όλα τα σημεία του Α,Β,Γ,κ.λπ.
Με το έμβολο που κλείνει ερμητικά τη φιάλη πιέζουμε την επιφάνεια του υγρού.Παρατηρούμε ότι το υγρό εκτοξεύεται με την ίδια ταχύτητα από όλες τις τρύπες.Το φαινόμενο αυτό αποτελεί μια ένδειξη ότι η πίεση που ασκήσαμε στο υγρό μεταδόθηκε σε όλα τα σημεία του αναλλοίωτη.
Το ίδιο συμβαίνει με την αντλία του γρύλου που χρησιμοποιούμε για να ανυψώνουμε τα αυτοκίνητα.Η πίεση που ασκούμε με το ένα έμβολο στο υγρό της αντλίας (p1) μεταδίδεται αναλλοίωτη στο μεγάλο έμβολο,δηλαδή έχουμε:
p1=p2
Την ιδιότητα των υγρών να μεταδίδουν την πίεση από σημείο σε σημείο τη μελέτησε αρχικά ο Γάλλος φυσικός Μπλαιζ Πασκάλ (Blaise Pascal) (1623-1662),που είναι γνωστή ως αρχή του Πασκάλ:
Η πίεση που προκαλείται σε υγρό που ισορροπεί μεταδίδεται αμετάβλητη σε όλα τα σημεία.
Στο ίδιο συμπέρασμα μπορούμε να καταλήξουμε και με τη σύριγγα του Πασκάλ που φαίνεται στο παρακάτω σχήμα.Όταν προκαλούμε πίεση στο υγρό με τη βοήθεια του εμβόλου,η πίεση αυτή μεταδίδεται σε όλα τα σημεία του υγρού και τα μανόμετρα δείχνουν την ίδια πίεση.
Φυσικά υπάρχει και η υδροστατική πίεση,η οποία αυξάνει με το βάθος,αλλά στο πείραμα αυτό τη θεωρούμε ασήμαντη.
Η Αρχή του Πασκάλ αφορά όλα τα ρευστά και είναι ένας από του βασικούς νόμους της Υδροστατικής.
Σε μία φιάλη τοποθετούμε χρωματισμένο υγρό(π.χ.νερό) και κλείνουμε τη φιάλη με ένα πώμα μέσα από το οποίο έχουμε περάσει μερικούς σωλήνες.Σημειώνουμε το ύψος του νερού που βρίσκεται στους σωλήνες προτού πιέσουμε την ελαστική σφαίρα Σ.Μετά πιέζουμε τη σφαίρα και παρατηρούμε ότι και στους τρεις σωλήνες το χρωματισμένο υγρό ανέρχεται κατά το ίδιο ύψος h.Αυτό σημαίνει ότι η πίεση,που δημιουργήθηκε στην ελεύθερη επιφάνεια του υγρού,μεταδόθηκε η ίδια σε όλα τα σημεία του Α,Β,Γ,κ.λπ.
.JPG) |
| Σε μία φιάλη τοποθετούμε χρωματισμένο υγρό(π.χ.νερό) και κλείνουμε τη φιάλη με ένα πώμα μέσα από το οποίο έχουμε περάσει μερικούς σωλήνες |
.jpg) |
| Η πίεση που προκαλείται σε υγρό που ισορροπεί μεταδίδεται αμετάβλητη σε όλα τα σημεία |
p1=p2
Την ιδιότητα των υγρών να μεταδίδουν την πίεση από σημείο σε σημείο τη μελέτησε αρχικά ο Γάλλος φυσικός Μπλαιζ Πασκάλ (Blaise Pascal) (1623-1662),που είναι γνωστή ως αρχή του Πασκάλ:
Η πίεση που προκαλείται σε υγρό που ισορροπεί μεταδίδεται αμετάβλητη σε όλα τα σημεία.
Στο ίδιο συμπέρασμα μπορούμε να καταλήξουμε και με τη σύριγγα του Πασκάλ που φαίνεται στο παρακάτω σχήμα.Όταν προκαλούμε πίεση στο υγρό με τη βοήθεια του εμβόλου,η πίεση αυτή μεταδίδεται σε όλα τα σημεία του υγρού και τα μανόμετρα δείχνουν την ίδια πίεση.
.JPG) |
| Στη σύριγγα του Πασκάλ όταν προκαλούμε πίεση στο υγρό με τη βοήθεια του εμβόλου,η πίεση αυτή μεταδίδεται σε όλα τα σημεία του υγρού |
.jpg) |
| Η Αρχή του Πασκάλ αφορά όλα τα ρευστά |
ΥΔΡΑΥΛΙΚΟ ΠΙΕΣΤΗΡΙΟ
Το υδραυλικό πιεστήριο χρησιμοποιείται στα ελαιοτριβεία για την εξαγωγή του λαδιού από τις ελιές,και σε διάφορα εργοστάσια για την κατασκευή πρεσσαριστών αντικειμένων.
Χρησιμοποιείται επίσης στη συμπίεση του βαμβακιού και αχύρου σε μπάλες,στη λειτουργία διάφορων γερανών.
.gif) |
| ΥΔΡΑΥΛΙΚΟ ΠΙΕΣΤΗΡΙΟ |
ΕΙΣΑΓΩΓΗ
Το υδραυλικό πιεστήριο είναι ένας υδραυλικός μηχανισμός που επιτρέπει την εφαρμογή μιας μεγάλης δύναμης ανύψωσης ή συμπίεσης.
Εφευρέτης του θεωρείται ο βρετανός μηχανικός Joseph Bramah.
Αρκετές φορές το υδραυλικό πιεστήριο ονομάζεται και πιεστήριο του Bramah.Τα υδραυλικά πιεστήρια αποτελούν την πιο διαδεδομένη μορφή πιεστηρίων στις μέρες μας.
ΜΕΛΕΤΗ ΤΟΥ ΥΔΡΑΥΛΙΚΟΥ ΠΙΕΣΤΗΡΙΟΥ
Το υδραυλικό πιεστήριο είναι ένας υδραυλικός μηχανισμός που επιτρέπει την εφαρμογή μιας μεγάλης δύναμης ανύψωσης ή συμπίεσης.
.gif) |
| Το υδραυλικό πιεστήριο είναι ένας υδραυλικός μηχανισμός που επιτρέπει την εφαρμογή μιας μεγάλης δύναμης ανύψωσης ή συμπίεσης |
Αρκετές φορές το υδραυλικό πιεστήριο ονομάζεται και πιεστήριο του Bramah.Τα υδραυλικά πιεστήρια αποτελούν την πιο διαδεδομένη μορφή πιεστηρίων στις μέρες μας.
ΜΕΛΕΤΗ ΤΟΥ ΥΔΡΑΥΛΙΚΟΥ ΠΙΕΣΤΗΡΙΟΥ
Τα βασικά μέρη ενός υδραυλικού πιεστηρίου είναι δύο κυλινδρικά δοχεία που συγκοινωνούν μεταξύ τους με λεπτό σωλήνα.Μέσα στα δοχεία κινούνται δύο έμβολα με διαφορετικά εμβαδά.
Όταν ασκήσουμε δύναμη F1 στο μικρό έμβολο που έχει εμβαδόν Α1,τότε παράγεται στο υγρό μία πίεση ίση με:
.JPG) |
| Τα βασικά μέρη ενός υδραυλικού πιεστηρίου είναι δύο κυλινδρικά δοχεία που συγκοινωνούν μεταξύ τους με λεπτό σωλήνα |
p=F1/A1
Σύμφωνα με την αρχή του Πασκάλ η πίεση αυτή μεταδίδεται αμετάβλητη σε όλα τα σημεία του υγρού.Άρα στη κάτω επιφάνεια του μεγάλου εμβόλου θα επικρατεί η ίδια πίεση p,της οποίας το αποτέλεσμα θα είναι η δύναμη F2.
Αν Α2 είναι το εμβαδόν του μεγάλου εμβόλου,τότε θα ισχύει η σχέση
p=F2/A2
Από τις σχέσεις p=F1/A1 και p=F2/A2 συνεπάγεται:
p=p
F2/A2=F1/A1
F2=F1• Α2/A1
F2/A2=F1/A1
F2=F1• Α2/A1
Από τον τελευταίο τύπο είναι φανερό ότι η δύναμη F2 είναι ανάλογη προς το Α2 και αντιστρόφως ανάλογη προς το Α1.
.JPG) |
| Η F2 είναι τόσες φορές μεγαλύτερη από την F1 όσες φορές είναι μεγαλύτερο το εμβαδόν του Α2 από το Α1 |
Αν επομένως θέλουμε να εξουδετερώσουμε μεγάλη αντίσταση F2,ασκώντας μικρή δύναμη F1,θα πρέπει να κάνουμε μεγάλο το εμβαδόν Α2 και μικρό το εμβαδόν Α1.
Αν το εμβαδόν του εμβόλου Α2 είναι διπλάσιο από το εμβαδόν του Α1,η δύναμη που ασκείται στο αυτοκίνητο είναι διπλάσια της δύναμης που ασκούμε με το χέρι μας .
.JPG) |
| Αν το εμβαδόν του εμβόλου Α2 είναι δεκαπλάσιο εμβαδόν από το εμβαδόν του Α1,τότε μπορούμε ασκώντας στο πρώτο έμβολο μία δύναμη 20 Ν,να μεταφέρει στο δεύτερο έμβολο δεκαπλάσια δύναμη,δηλαδή F2=200 Ν |
Αν το εμβαδόν του εμβόλου Α2 είναι δεκαπλάσιο εμβαδόν από το εμβαδόν του Α1,τότε μπορούμε ασκώντας στο πρώτο έμβολο μία δύναμη 20 Ν,να μεταφέρει στο δεύτερο έμβολο δεκαπλάσια δύναμη,δηλαδή F2=200 Ν.
Γενικά,η F2 είναι τόσες φορές μεγαλύτερη από την F1 όσες φορές είναι μεγαλύτερο το εμβαδόν του Α2 από το Α1.Σε αυτό το σημείο πρέπει να προσέξουμε τη διαφορά μεταξύ πίεσης και δύναμης.Σε μια υδραυλική αντλία ή πιεστήριο η πίεση διατηρείται σταθερή,ενώ η δύναμη πολλαπλασιάζεται.
ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΥΔΡΑΥΛΙΚΟΥ ΠΙΕΣΤΗΡΙΟΥ
ΕΦΑΡΜΟΓΕΣ ΤΟΥ ΥΔΡΑΥΛΙΚΟΥ ΠΙΕΣΤΗΡΙΟΥ
Το υδραυλικό πιεστήριο,λοιπόν,είναι ένα είδος υδραυλικού μοχλού,δηλαδή ένα σύστημα που πολλαπλασιάζει τη δύναμη που ασκούμε στο μικρό έμβολο.
.JPG) |
| Ένα μεγάλο υδραυλικό πιεστήριο που χρησιμοποιείται στην βιομηχανία |
.JPG) |
| Το υδραυλικό πιεστήριο χρησιμοποιείται επίσης στη συμπίεση του βαμβακιού |
ΥΔΡΑΥΛΙΚΟΣ ΑΝΥΨΩΤΗΡΑΣ ΑΥΤΟΚΙΝΗΤΩΝ
ΠΙΕΣΗ ΣΕ ΥΓΡΟ
Η ελεύθερη επιφάνεια των υγρών βρίσκεται πάντα κάτω από κάποια εξωτερική πίεση που συνήθως είναι η ατμοσφαιρική πίεση.
Σύμφωνα με την αρχή του Πασκάλ η εξωτερική πίεση pατμ μεταδίδεται αμετάβλητη σε όλα τα σημεία του υγρού.Εξ άλλου,σε κάθε σημείο του υγρού υπάρχει υδροστατική πίεση.
Επομένως η συνολική πίεση pολ σε ένα σημείο που βρίσκεται σε βάθος h από την ελεύθερη επιφάνειά του,είναι ίση με το άθροισμα της εξωτερικής ατμοσφαιρικής pατμ και της υδροστατικής πίεσης ρ·g·h.Άρα η ολική πίεση pολ δίνεται από τη σχέση:
pολ=pεξ+ρ·g·h
ΣΤΡΩΤΗ ΡΟΗ
ΤΥΡΒΩΔΗΣ ΡΟΗ
Όταν όμως η ταχύτητα υπερβεί τη λεγόμενη κρίσιμη ταχύτητα και οι δυνάµεις µεταξύ των µορίων του ρευστού (ιξώδες ) αλλά και µεταξύ των µορίων του ρευστού και των τοιχωµάτων του σωλήνα δηµιουργεί κατά τη ροή του δίνες,τότε η ροή γίνεται τυρβώδης ή στροβιλώδης ή μη στάσιμη ροή.
Τυρβώδης ροή ή στροβιλώδης ή μη στάσιμη ροή ονομάζεται το συγκεκριμένο είδος ροής των ρευστών που χαρακτηρίζεται από χαώδεις ή τυχαίες μεταβολές του πεδίου ροής αυτών.
Στην τυρβώδη ροή όµως που δεν υπάρχει εικόνα µόνιµης κατάστασης η ροή γίνεται ακανόνιστη και χαοτική και µόρια του ρευστού διαπερνούν τις συνοριακές επιφάνειες των σωλήνων ροής .
Η τυρβώδης ροή δεν είναι στρωτή,είναι άτακτη,ακανόνιστη και χαρακτηρίζεται από περιοχές που δίνουν την εντύπωση μικρών στροβίλων.Έτσι οι μεταβλητές του πεδίου ροής ενός ρευστού,πίεση και ταχύτητα,μεταβάλλονται απότομα και τυχαία για κάθε σημείο του χώρου που καταλαμβάνει το πεδίο ροής και κατά τη χρονική εξέλιξη του φαινομένου.
Κατά τη τυρβώδη ροή οι γραμμές ροής του ρευστού λαμβάνουν μορφή ακανόνιστων καμπυλών οι οποίες τέμνουν συνεχώς αλλήλους,δίνοντας έτσι την εικόνα ροής με στροβιλισμούς.
ΠΡΑΓΜΑΤΙΚΑ ΡΕΥΣΤΑ
Όμως στην πραγματικότητα η συμπεριφορά των κινούμενων ρευστών διαφέρει πολύ ή λίγο από τη συμπεριφορά των ιδανικών ρευστών.
Άρα η ταχύτητά του μορίου του ρευστού έχει σε κάθε θέση πάντοτε τη διεύθυνση της εφαπτομένης στην ρευματική γραμμή που διέρχεται από το σημείο αυτό.Δύο ρευματικές γραμμές δεν είναι δυνατόν να τέμνονται ποτέ όταν η ροή είναι στρωτή,διότι αν τέμνονταν,τότε κάθε μόριο του ρευστού στο σημείο τομής θα μπορούσε να ακολουθήσει ή τη μία τροχιά ή την άλλη και έτσι η ροή δεν θα ήταν στρωτή.
ΦΛΕΒΑ
.JPG) |
| H συνολική πίεση pολ σε ένα σημείο που βρίσκεται σε βάθος h από την ελεύθερη επιφάνειά του,είναι ίση με το άθροισμα της εξωτερικής ατμοσφαιρικής pατμ και της υδροστατικής πίεσης ρ·g·h |
.jpg) |
| Η πίεση στο Α είναι: pA=pεξ+ρ·g·h |
pολ=pεξ+ρ·g·h
ΑΝΩΣΗ-ΑΡΧΗ ΤΟΥ ΑΡΧΙΜΗΔΗ
Άρα:
Άρα βρίσκουμε το βάρος του στον αέρα.Ας υποθέσουμε ότι το βάρος αυτό είναι 10 Ν.
Η άνωση είναι ανεξάρτητη από το σχήμα και το βάρος του σώματος που είναι βυθισμένο αλλά και από το βάθος στο οποίο βρίσκεται το σώμα και εξαρτάται μονάχα από τα μεγέθη τα οποία εμφανίζονται στον μαθηματικό της τύπο δηλαδή από την πυκνότητα του ρευστού,την επιτάχυνση της βαρύτητας και από τον όγκο του σώματος ο οποίος είναι βυθισμένος στο ρευστό.
Όταν βάρος σώματος είναι μικρότερο του βάρους του εκτοπίσματος του, τότε το σώμα ανέρχεται.
.JPG) |
| ΑΝΩΣΗ-ΑΡΧΗ ΤΟΥ ΑΡΧΙΜΗΔΗ |
ΕΙΣΑΓΩΓΗ
Αν βυθίσουμε σε νερό ή κάποιο άλλο υγρό μία ελαστική μπάλα και την αφήσουμε ελεύθερη,παρατηρούμε ότι ανεβαίνει γρήγορα στην επιφάνεια.
Επίσης,αν δοκιμάσουμε να βυθίσουμε στο νερό ένα άδειο κύπελλο,αισθανόμαστε μία δύναμη από το νερό,που ωθεί το δοχείο προς τα πάνω.
 |
| H άνωση σπρώχνει το μπαλόνι προς τα πάνω |
Όταν κολυμπάμε διατηρούμε το σώμα μας στην επιφάνεια της θάλασσας.Τα πλοία επιπλέουν στη επιφάνεια της θάλασσας,της λίμνης ή των ποταμών όταν ταξιδεύουν.Ένα μπαλόνι που κρατάει ένα παιδάκι αιωρείται.
Είναι πιο εύκολο να σηκώσουμε μια πέτρα όταν αυτή είναι βυθισμένη μέσα στο νερό απ' ότι όταν βρίσκεται έξω από αυτό.Σχηματίζουμε την εντύπωση ότι το βάρος της πέτρας ελαττώνεται όταν τη βυθίζουμε στο νερό.
Είναι πιο εύκολο να σηκώσουμε μια πέτρα όταν αυτή είναι βυθισμένη μέσα στο νερό απ' ότι όταν βρίσκεται έξω από αυτό.Σχηματίζουμε την εντύπωση ότι το βάρος της πέτρας ελαττώνεται όταν τη βυθίζουμε στο νερό.
.jpg) |
| Κρεμάμε από ένα δυναμόμετρο τη πέτρα.Παρατηρούμε ότι η ένδειξη του δυναμομέτρου όταν η πέτρα είναι μέσα στο νερό είναι μικρότερη από την ένδειξη όταν η πέτρα είναι στον αέρα |
Κρεμάμε από ένα δυναμόμετρο τη πέτρα.Παρατηρούμε ότι η ένδειξη του δυναμομέτρου όταν η πέτρα είναι μέσα στο νερό είναι μικρότερη από την ένδειξη όταν η πέτρα είναι στον αέρα.Εδώ πρέπει να ξεκαθαρίσουμε ότι το βάρος της πέτρας, δηλαδή η βαρυτική δύναμη που η γη ασκεί στην πέτρα,είναι η ίδια είτε η πέτρα βρίσκεται μέσα στο νερό είτε βρίσκεται στον αέρα.Το βάρος ενός σώματος όπως ξέρουμε δεν είναι τίποτε άλλο παρά η ελκτική δύναμη από τη Γη στο σώμα και δεν μεταβάλλεται πρακτικά για μικρές υψομετρικές αλλαγές.
ΕΝΝΟΙΑ ΤΗΣ ΑΝΩΣΕΩΣ
ΕΝΝΟΙΑ ΤΗΣ ΑΝΩΣΕΩΣ
Όλα τα παραπάνω παραδείγματα οφείλονται σε μία δύναμη που ονομάζεται άνωση.Άνωση ασκείται και στα σώματα που βρίσκονται μέσα στον αέρα.
.JPG) |
| Σε κάθε σώμα που βρίσκεται μέσα σε υγρό,ασκείται από το υγρό μία δύναμη κατακόρυφη και με φορά από κάτω προς τα πάνω.Η δύναμη αυτή ονομάζεται άνωση |
Σε κάθε σώμα που βρίσκεται μέσα σε υγρό,ασκείται από το υγρό μία δύναμη κατακόρυφη και με φορά από κάτω προς τα πάνω.
Η δύναμη αυτή ονομάζεται άνωση.
Η δύναμη αυτή ονομάζεται άνωση.
ΜΕΤΡΗΣΗ ΤΗΣ ΑΝΩΣΕΩΣ
Κρεμάμε από το άγκιστρο δυναμομέτρου μία πέτρα.Η ένδειξη του δυναμομέτρου,Wφ,που την ονομάζουμε φαινόμενο βάρος,είναι ίση με το μέτρο της δύναμης που ασκεί το δυναμόμετρο στην πέτρα.Η πέτρα ισορροπεί.Έτσι,όταν βρίσκεται στον αέρα,ισχύει:
Wφ=W
Άρα βρίσκουμε το βάρος του στον αέρα.Ας υποθέσουμε ότι το βάρος αυτό είναι 10 Ν.
Κατόπιν βυθίζουμε το σώμα σε νερό και παρατηρούμε ότι η ένδειξη του δυναμομέτρου ελαττώνεται και γίνεται π.χ. 6 Ν.Είναι φανερό πως η μείωση στην ένδειξη του δυναμομέτρου οφείλεται στην άνωση,η οποία ωθεί το σώμα προς τα πάνω.
Άρα η άνωση του σώματος αυτού είναι 4 Ν.
W'φ+A=W
δηλαδή
W'φ=W-Α.
Άρα η άνωση του σώματος αυτού είναι 4 Ν.
W'φ+A=W
δηλαδή
W'φ=W-Α.
Άρα η άνωση του σώματος αυτού είναι 4 Ν.
Επομένως,η δύναμη που ασκεί το δυναμόμετρο στην πέτρα προκύπτει ως η συνισταμένη του βάρους της πέτρας (W),που έχει φορά προς τα κάτω και της άνωσης Α,που έχει φορά προς τα επάνω.
Επομένως,η δύναμη που ασκεί το δυναμόμετρο στην πέτρα προκύπτει ως η συνισταμένη του βάρους της πέτρας (W),που έχει φορά προς τα κάτω και της άνωσης Α,που έχει φορά προς τα επάνω.
ΕΞΗΓΗΣΗ ΤΗΣ ΑΝΩΣΗΣ
Θεωρούμε έναν κύβο βυθισμένο σε υγρό.Το υγρό ασκεί δύναμη στον κύβο η οποία οφείλεται στην υδροστατική πίεση.Έτσι, στην κάτω επιφάνεια του κύβου εμβαδού Α ασκείται δύναμη FA=pA·A και στην επάνω FB=pB·A.
Σύμφωνα με το νόμο της υδροστατικής,στην κάτω επιφάνεια του κύβου επικρατεί μεγαλύτερη πίεση απ' ότι στην επάνω,δηλαδή:
pA>pB
και επομένως
FA>FB
Η συνισταμένη όλων των δυνάμεων που ασκείται από το υγρό στον κύβο λόγω της υδροστατικής πίεσης έχει κατακόρυφη διεύθυνση και φορά προς τα πάνω.Η συνισταμένη αυτή δύναμη είναι η άνωση.
.JPG) |
| Στην κάτω επιφάνεια του κύβου επικρατεί μεγαλύτερη πίεση απ' ότι στην επάνω,δηλαδή pA>pB και επομένως FA>FB |
pA>pB
και επομένως
FA>FB
Η συνισταμένη όλων των δυνάμεων που ασκείται από το υγρό στον κύβο λόγω της υδροστατικής πίεσης έχει κατακόρυφη διεύθυνση και φορά προς τα πάνω.Η συνισταμένη αυτή δύναμη είναι η άνωση.
ΠΑΡΑΓΟΝΤΕΣ ΠΟΥ ΕΞΑΡΤΑΤΑΙ Η ΑΝΩΣΗ
Τώρα θα εξετάσουμε από ποιους παράγοντες εξαρτάται η άνωση.Θα εκτελέσουμε ένα πείραμα.Παίρνουμε δύο κομμάτια πλαστελίνης ίδιου βάρους.Στο ένα δίνουμε το σχήμα κύβου και στο άλλο σφαίρας.Ύστερα τα βυθίζουμε πλήρως στο ίδιο υγρό στο ίδιο βάθος.Μετράμε την άνωση στα δυο σώματα.Παρατηρούμε ότι είναι ίδια.Αντικαθιστούμε τη σφαίρα από πλαστελίνη με μεταλλική ίδιας ακτίνας και μετράμε τις δύο ανώσεις.
Παρατηρούμε ότι είναι ίδιες.Από αυτά τα αποτελέσματα συμπεραίνουμε ότι η άνωση δεν εξαρτάται από το σχήμα και το βάρος του σώματος που βυθίζεται.Βυθίζουμε το ένα από τα δύο σώματα σε μεγαλύτερο βάθος και παρατηρούμε ότι η άνωση δε μεταβάλλεται.Συμπεραίνουμε ότι,εφόσον το σώμα είναι ολόκληρο βυθισμένο στο υγρό,η άνωση είναι ανεξάρτητη του βάθους στο οποίο βρίσκεται.
.JPG) |
| Το υγρό με τη μεγαλύτερη πυκνότητα ασκεί στο σώμα μεγαλύτερη άνωση |
.JPG) |
| Το λάδι έχει μεγαλύτερη πυκνότητα από το νερό.Άρα το λάδι ασκεί μεγαλύτερη άνωση σε ένα σώμα από το νερό |
Γνωρίζουμε ότι επιπλέουμε πιο εύκολα στη θάλασσα απ' ότι σε μια λίμνη ή πισίνα.Αυτό συμβαίνει γιατί το νερό της θάλασσας,που αποτελείται από αλατόνερο έχει μεγαλύτερη πυκνότητα από το νερό της λίμνης που είναι καθαρό νερό.
.JPG) |
Η σειρά των υγρών σε μια στήλη |
Βυθίζουμε πλήρως στο ίδιο υγρό δύο κύβους,έναν αλουμινένιο και ένα σιδερένιο ίδιου βάρους.Ο κύβος από αλουμίνιο έχει μεγαλύτερο όγκο.Διαπιστώνουμε ότι η άνωση που ασκείται στο σιδερένιο κύβο είναι μικρότερη, από αυτή που ασκείται στον αλουμινένιο.Βυθίζουμε σταδιακά τον έναν από τους κύβους στο υγρό.Παρατηρούμε ότι όσο περισσότερο μέρος του όγκου ενός σώματος βυθίζουμε μέσα στο υγρό,τόσο αυξάνεται η άνωση που ασκείται στο σώμα.
ΜΕΤΡΗΣΗ ΤΟΥ ΒΑΡΟΥΣ ΤΟΥ ΝΕΡΟΥ ΠΟΥ ΕΚΤΟΠΙΖΕΤΑΙ
Όταν το σώμα βυθίζεται στο νερό,η στάθμη του νερού ανεβαίνει.Αυτό σημαίνει ότι το σώμα εκτοπίζεται κάποια ποσότητα νερού.Για να μετρήσουμε το βάρος του νερού που εκτοπίζεται από το σώμα,χρησιμοποιούμε ειδικό δοχείο που φέρει στα πλάγια του ένα μικρό σωλήνα.
Γεμίζουμε το δοχείο μέχρι το χείλος του σωλήνα και βυθίζουμε το σώμα στο νερό.Μαζεύουμε το νερό που εκτοπίζεται σε ένα δοχείο και το ζυγίζουμε.Από τη ζύγιση προκύπτει ότι το βάρος του νερού που εκτοπίζεται είναι 4 Ν.Άρα η άνωση (4 Ν) είναι ίση με το βάρος του νερού που εκτοπίζεται (4 Ν).Στο ίδιο συμπέρασμα καταλήγουμε και αν χρησιμοποιήσουμε ένα άλλο οποιοδήποτε υγρό.
ΑΡΧΗ ΤΟΥ ΑΡΧΙΜΗΔΗ
Ο Έλληνας μαθηματικός και φυσικός Αρχιμήδης (3ος αιώνας π.Χ.),πρώτος παρατήρησε ότι όταν ένα σώμα βυθίζεται στο υγρό,καταλαμβάνει χώρο στον οποίο προηγουμένως υπήρχε υγρό.Δηλαδή το σώμα εκτοπίζει το υγρό, οπότε η στάθμη του υγρού ανεβαίνει.Ο όγκος του υγρού που εκτοπίζεται ισούται με τον όγκο του σώματος που είναι βυθισμένο σ' αυτό.
Καταλήγουμε ότι η άνωση αυξάνεται,όταν αυξάνεται ο όγκος του υγρού που εκτοπίζεται από το σώμα,που βυθίζουμε σ' αυτό.
Ο Αρχιμήδης συγκέντρωσε όλες τις παραπάνω παρατηρήσεις και διατύπωσε μια πρόταση που είναι γνωστή ως αρχή του Αρχιμήδη:
.JPG) |
| Κάθε σώμα,που βυθίζεται σε υγρό που ισορροπεί,δέχεται τόση άνωση όσο είναι το βάρος του υγρού που εκτοπίζεται από το σώμα |
Τα υγρά ασκούν δύναμη σε κάθε σώμα που βυθίζεται μέσα σε αυτά.Η δύναμη αυτή ονομάζεται άνωση,είναι κατακόρυφη,με φορά προς τα πάνω και το μέτρο της ισούται με το βάρος του υγρού που εκτοπίζεται από το σώμα.
Μία πιο απλή διατύπωση της αρχής του Αρχιμήδη είναι:
Κάθε σώμα,που βυθίζεται σε υγρό που ισορροπεί,δέχεται τόση άνωση όσο είναι το βάρος του υγρού που εκτοπίζεται από το σώμα.
Η αρχή του Αρχιμήδη ισχύει και για σώματα που βρίσκονται σε αέρια.Η μαθηματική έκφραση του νόμου είναι:
Α=ρυγρού•g•Vβυθ
όπoυ:
Α η άνωση που ασκείται σε σώμα βυθισμένο σε υγρό (ή αέριο) την οποία μετράμε σε Ν αφού είναι δύναμη,
ρυγρού η πυκνότητα του υγρού την οποία μετράμε σε Kg/m3 και
Vβυθ ο όγκος (ή το μέρος του όγκου) του σώματος που είναι βυθισμένο στο υγρό (ή το αέριο) την οποία μετράμε σε m3.
Η άνωση είναι η συνισταμένη δύναμη όλων των δυνάμεων που δέχεται το σώμα λόγω της υδροστατικής πίεσης και έχει κατακόρυφη διεύθυνση και φορά προς τα πάνω.
.JPG) |
| Η ανύψωση ενός υποβρυχίου λόγω της Αρχής του Αρχιμήδη |
Όταν βάρος σώματος είναι μεγαλύτερο του βάρους του εκτοπίσματος του,τότε το σώμα βυθίζεται.
.JPG) |
| Tα πλοία υπακούουν στην Αρχή του Αρχιμήδη |
Συνεπώς όσο μεγαλύτερο το βάρος του εκτοπίσματος από το βάρος του σώματος τόσο μεγαλύτερη και η άνωση που δέχεται το σώμα.
Το σημείο εφαρμογής της ανώσεως λέγεται κέντρο ανώσεως και όπως αποδεικνύεται,συμπίπτει με το κέντρο βάρους του υγρού που εκτοπίζεται από το σώμα.
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΑΡΧΗΣ ΤΟΥ ΑΡΧΙΜΗΔΗ
ΕΦΑΡΜΟΓΕΣ ΤΗΣ ΑΡΧΗΣ ΤΟΥ ΑΡΧΙΜΗΔΗ
Η Αρχή του Αρχιμήδη έχει πολύ μεγάλη εφαρμογή στη καθημερινή ζωή κυρίως στη Τεχνική.Οτιδήποτε που πλέει,όπως τα πλοία,όλα τα ελαφρύτερα του ύδατος σώματα,το ανθρώπινο σώμα,οι πλωτήρες,αμφίβια οχήματα κ.λπ υπακούουν στην Αρχή αυτή.
Περισσότερο όμως ενδιαφέρει η Αρχή αυτή την Ναυπηγική,δηλαδή την επιστήμη που ασχολείται στη κατασκευή των πλοίων.Εκεί η Αρχή του Αρχιμήδη μελετάται,αναλύεται και εφαρμόζεται σε όλες τις λεπτομέρειές της.
.JPG) |
| Η ανύψωση ενός υποβρυχίου |
.JPG) |
| Μέγιστη εφαρμογή της Αρχής του Αρχιμήδη παρατηρείται στα Υποβρύχια |
Μέγιστη εφαρμογή της Αρχής του Αρχιμήδη παρατηρείται στα Υποβρύχια και στις Πλωτές Δεξαμενές που μεταβάλουν συνεχώς τις τιμές πλευστότητας τους.
ΙΣΤΟΡΙΑ ΤΗΣ ΑΡΧΗΣ ΤΟΥ ΑΡΧΙΜΗΔΗ
Μία μέρα,ο βασιλιάς Ιέρων Α' των Συρακουσών παρήγγειλε στο μεγαλύτερο καλλιτέχνη της πόλης να του φτιάξει μία κορώνα από καθαρό χρυσάφι.Όταν ο βασιλιάς πήρε την κορώνα,άρχισαν να διαδίδονται φήμες πως ο καλλιτέχνης τον είχε κοροϊδέψει,παίρνοντας ένα μέρος από το χρυσάφι και αντικαθιστώντας το με άλλο μέταλλο.Ωστόσο,η τελειωμένη κορώνα είχε το ίδιο βάρος με το χρυσάφι του βασιλιά.
Ο βασιλιάς κάλεσε τότε τον Αρχιμήδη να εξετάσει το ζήτημα.Στα πειράματά του,ο Αρχιμήδης βρήκε το νόμο του ειδικού βάρους.Ανακάλυψε πως όταν ένα στερεό σώμα μπει μέσα σε υγρό χάνει τόσο βάρος όσο είναι το βάρος του όγκου του νερού που εκτοπίζει.
 |
| Ο Αρχιμήδης και η κορώνα από καθαρό χρυσάφι του βασιλιά Ιέρων Α' των Συρακουσών |
 |
| Ο Αρχιμήδης επινόησε το σύστημα να παίρνει το ειδικό βάρος των στερεών σωμάτων |
Ο Αρχιμήδης επινόησε το σύστημα να παίρνει το ειδικό βάρος των στερεών σωμάτων.Ζύγιζε πρώτα το στερεό στον αέρα και έπειτα το ζύγιζε μέσα στο νερό.Και αφού το στερεό ζύγιζε λιγότερο μέσα στο νερό, αφαιρούσε το βάρος που είχε μέσα στο νερό από το βάρος που είχε στον αέρα.
Τέλος,διαιρούσε το βάρος του στερεού σώματος στον αέρα με την απώλεια βάρους που είχε το σώμα μέσα στο νερό.Έμαθε έτσι,πως ένας δοσμένος όγκος από χρυσάφι ζυγίζει 19,3 φορές τον ίσο όγκο νερού.
 |
| Ο Αρχιμήδης μπορεί να είχε χρησιμοποιήσει την αρχή της πλευστότητας για να καθοριστεί αν η χρυσή κορώνα ήταν λιγότερο πυκνή από το ατόφιο χρυσάφι |
| Ο Αρχιμήδης δεν βρήκε το πρόβλημα της βασιλικής κορώνας και σηκώθηκε να πάει στα λουτρά για να ξεκουραστεί |
Όμως,καθώς δεν μπόρεσε να προχωρήσει περισσότερο στο πρόβλημα της βασιλικής κορώνας,ο Αρχιμήδης σηκώθηκε να πάει στα λουτρά για να ξεκουραστεί.
Εκεί βρήκε τη λύση.Μέσα στον ενθουσιασμό του βγήκε από το λουτρό γυμνός στο δρόμο φωνάζοντας:
"Εύρηκα! Εύρηκα!"
Ο Αρχιμήδης γύρισε στο σπίτι του,ζύγισε την κορώνα στον αέρα και ύστερα τη ζύγισε μέσα στο νερό.Με τη μέθοδο αυτή βρήκε το ειδικό βάρος της κορώνας.Το ειδικό βάρος της δεν ήτανε 19,3.Δεν μπορούσε,λοιπόν,η κορώνα να είναι από καθαρό χρυσάφι.Ο Αρχιμήδης απέδειξε πως ο καλλιτέχνης ήταν απατεώνας.
| Ο Αρχιμήδης βρήκε τη λύση στα λουτρά .Μέσα στον ενθουσιασμό του βγήκε από το λουτρό γυμνός στο δρόμο φωνάζοντας: "Εύρηκα! Εύρηκα!". |
"Εύρηκα! Εύρηκα!"
Ο Αρχιμήδης γύρισε στο σπίτι του,ζύγισε την κορώνα στον αέρα και ύστερα τη ζύγισε μέσα στο νερό.Με τη μέθοδο αυτή βρήκε το ειδικό βάρος της κορώνας.Το ειδικό βάρος της δεν ήτανε 19,3.Δεν μπορούσε,λοιπόν,η κορώνα να είναι από καθαρό χρυσάφι.Ο Αρχιμήδης απέδειξε πως ο καλλιτέχνης ήταν απατεώνας.
ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ
 |
| ΡΕΥΣΤΑ ΣΕ ΚΙΝΗΣΗ |
ΕΙΣΑΓΩΓΗ
Η μελέτη των ρευστών που κάναμε μέχρι τώρα περιοριζόταν σε ακίνητα ρευστά.Τώρα όμως θα μελετήσουμε ρευστά που κινούνται.Αλλά αντί να προσπαθήσουμε να μελετήσουμε την κίνηση κάθε μορίου του ρευστού ως συνάρτηση του χρόνου,θα ακολουθήσουμε τον συνήθη τρόπο και θα περιγράψουμε τις ιδιότητες του ρευστού σε κάθε σημείο του συναρτήσει του χρόνου.
Κατά την κίνηση των ρευστών αναπτύσσονται δυνάμεις τριβής μεταξύ των μορίων τους.Οι δυνάμεις αυτές ονομάζονται εσωτερικές τριβές.
Επίσης αναπτύσσονται δυνάμεις και μεταξύ των μορίων τους και των τοιχωμάτων του σωλήνα μέσα στον οποίο πραγματοποιείται η κίνηση.Οι δυνάμεις αυτές ονομάζονται δυνάμεις συνάφειας.
.jpg) |
| Κατά την κίνηση των ρευστών αναπτύσσονται δυνάμεις τριβής μεταξύ των μορίων τους αλλά και μεταξύ των μορίων τους και των τοιχωμάτων του σωλήνα μέσα στον οποίο πραγματοποιείται η κίνηση |
Επίσης αναπτύσσονται δυνάμεις και μεταξύ των μορίων τους και των τοιχωμάτων του σωλήνα μέσα στον οποίο πραγματοποιείται η κίνηση.Οι δυνάμεις αυτές ονομάζονται δυνάμεις συνάφειας.
ΣΤΡΩΤΗ ΡΟΗ
Όταν ένα ρευστό κινείται,η κίνηση του περιγράφεται ως μια από δυο είδη κίνησης.Όταν κάθε μόριο του ρευστού ακολουθεί στρωτή τροχιά,οι τροχιές των μορίων δεν τέμνονται.Αν η συνολική εικόνα της ροής δεν αλλάζει µε το χρόνο λέμε ότι η ροή είναι στρωτή ή στάσιμη ή μόνιμη.
 |
| Στρωτή ή στάσιμη ή μόνιμη ροή ονομάζεται η ροή που μπορεί να περιγραφτεί με την παραδοχή ότι το ρευστό αποτελείται από πολλά λεπτά στρώματα που ολισθαίνουν το ένα πάνω στο άλλο |
Στρωτή ή στάσιμη ή μόνιμη ροή ονομάζεται η ροή που μπορεί να περιγραφτεί με την παραδοχή ότι το ρευστό αποτελείται από πολλά λεπτά στρώματα που ολισθαίνουν το ένα πάνω στο άλλο.
 |
| Στην στρωτή ροή,η ταχύτητα του ρευστού σε κάθε σημείο του χώρου παραμένει σταθερή ως προς τον χρόνο |
Έτσι στην στρωτή ροή,η ταχύτητα του ρευστού σε κάθε σημείο του χώρου παραμένει σταθερή ως προς τον χρόνο.
 |
| Στη στρωτή ροή τα σωµατίδια του ρευστού κινούνται κατά µήκος παραλλήλων τροχιών,σε στρώµατα. |
Η στρωτή ροή ενός ρευστού δεν παρουσιάζει στροβίλους.Στη στρωτή ροή τα σωµατίδια του ρευστού κινούνται κατά µήκος παραλλήλων τροχιών,σε στρώµατα.Τα µεγέθη των ταχυτήτων γειτονικών στρωµάτων δεν είναι ίσα.
 |
| Εικόνα παράλληλης ροής είναι εκείνη του νερού από τις βρύσες |
Κατά την στρωτή ροή το ρευστό ρέει σε παράλληλες προς τον άξονα του αγωγού γραμμές δίνοντας έτσι την εικόνα της ομαλής ή στρωτής ροής.Συνήθης εικόνα παράλληλης ροής είναι εκείνη του νερού από τις βρύσες.
 |
| Παράδειγμα στρωτής ροής |
Για στρωτή ροή ισχύει,πάντα είτε το ρευστό είναι ασυµπίεστο είτε συµπιεστό:
Δm1=Δm2
ΤΥΡΒΩΔΗΣ ΡΟΗ
Όταν όμως η ταχύτητα υπερβεί τη λεγόμενη κρίσιμη ταχύτητα και οι δυνάµεις µεταξύ των µορίων του ρευστού (ιξώδες ) αλλά και µεταξύ των µορίων του ρευστού και των τοιχωµάτων του σωλήνα δηµιουργεί κατά τη ροή του δίνες,τότε η ροή γίνεται τυρβώδης ή στροβιλώδης ή μη στάσιμη ροή.
 |
| Τυρβώδης ροή ή στροβιλώδης ή μη στάσιμη ροή ονομάζεται το συγκεκριμένο είδος ροής των ρευστών που χαρακτηρίζεται από χαώδεις ή τυχαίες μεταβολές του πεδίου ροής αυτών |
 |
| Η τυρβώδης ροή είναι άτακτη,ακανόνιστη και χαρακτηρίζεται από περιοχές που δίνουν την εντύπωση μικρών στροβίλων |
 |
| Κατά τη τυρβώδη ροή οι γραμμές ροής του ρευστού λαμβάνουν μορφή ακανόνιστων καμπυλών δίνοντας έτσι την εικόνα ροής με στροβιλισμούς |
 |
| Εικόνα τυρβώδους ροής |
.jpg) |
| Προσομοίωση τυρβώδους ροής ενός κυλινδρικού εμποδίου |
Λογουχάρη,η ροή του νερού σε ένα ρυάκι γίνεται τυρβώδης εκεί όπου το νερό συναντά βράχια ή άλλα εμπόδια,οπότε αρχίζει να αφρίζει και να στριφογυρίζει.
Εικόνες τυρβώδους ροής μας παρέχουν οι ποταμοί όταν παρουσιάζουν στροβίλους που μπορεί να οφείλονται σε υποκείμενα ρεύματα,σε τριβές σε βραχώδεις όχθες ή σε πετρώματα του βυθού ή σε απότομη στένωση του πλάτους τους.
Τυρβώδη ροή επίσης είναι δυνατόν να προκαλέσουν και πλοία που κινούνται ενάντια στο ρεύμα του ποταμού καθώς επίσης και οι αεροστρόβιλοι που μπορεί να επηρεάσουν την άνωση του αεροπλάνου με συνέπεια να προκληθούν τρανταγμοί του σκάφους.
 |
| Εικόνες τυρβώδους ροής μας παρέχουν οι ποταμοί όταν παρουσιάζουν στροβίλους |
 |
| Τυρβώδη ροή επίσης είναι δυνατόν να προκαλέσουν και οι αεροστρόβιλοι που μπορεί να επηρεάσουν την άνωση του αεροπλάνου |
.jpg) |
| Ρίχνοντας χρώματα μέσα σε ένα ρευστό που κάνει τυρβώδη ροή έχουμε μια εικόνα των δινών που σχηματίζει |
Το φαινόμενο έχει πολύ μεγάλη πρακτική και τεχνολογική σημασία,για παράδειγμα οι ιδιότητες μεταφοράς θερμότητας αλλάζουν δραστικά κατά τη μετάβαση από γραμμική σε τυρβώδη ροή.Τούτο επιδρά για παράδειγμα στο σχεδιασμό βιομηχανικών συστημάτων μεταφοράς θερμότητας όπως οι εναλλάκτες θερμότητας στη χημική βιομηχανία.
ΑΣΥΜΠΙΕΣΤΟ ΡΕΥΣΤΟ
Ασυµπίεστο ονομάζεται ένα ρευστό που έχει σταθερό όγκο,ανεξάρτητα από την πίεση.
Επειδή όµως και η µάζα του ρευστού είναι σταθερή έχουμε:
ρ=m/V=σταθ.
Δηλαδή αυτό σηµαίνει πως σ’ ένα ασυµπίεστο ρευστό η πυκνότητα του είναι η ίδια σ’ όλη την έκταση του.
ΑΣΥΜΠΙΕΣΤΟ ΡΕΥΣΤΟ
Ασυµπίεστο ονομάζεται ένα ρευστό που έχει σταθερό όγκο,ανεξάρτητα από την πίεση.
 |
| Ασυµπίεστο ονομάζεται ένα ρευστό που έχει σταθερό όγκο,ανεξάρτητα από την πίεση |
ρ=m/V=σταθ.
Δηλαδή αυτό σηµαίνει πως σ’ ένα ασυµπίεστο ρευστό η πυκνότητα του είναι η ίδια σ’ όλη την έκταση του.
ΙΔΑΝΙΚΟ ΡΕΥΣΤΟ
Ο όρος ιξώδες περιγράφει την εσωτερική τριβή του ρευστού.Η εσωτερική τριβή του ρευστού περιγράφει την τριβή ανάμεσα σε δυο συνεχόμενες ''στρώσεις'' του ρευστού όταν η μια κινείται σε σχέση με την άλλη.Λόγω του ιξώδους,μέρος της κινητικής ενέργειας μετατρέπεται σε θερμική.Η διαδικασία είναι παρόμοια με την περίπτωση κατά την οποία ένα αντικείμενο κινείται πάνω σε τραχιά οριζόντια επιφάνεια χάνοντας κινητική ενέργεια.
 |
| Λόγω του ιξώδους,μέρος της κινητικής ενέργειας μετατρέπεται σε θερμική |
Η κίνηση των ρευστών είναι γενικά πρόβλημα περίπλοκο.Και γι'αυτό θα κάνουμε ορισμένες υποθέσεις οι οποίες θα απλουστεύσουν τη μελέτη μας.Όπως θα δούμε,πολλά προβλήματα της κίνησης των ρευστών μπορούμε να τα κατανοήσουμε καλύτερα εάν μελετήσουμε πρώτα την κίνηση ενός ιδανικού ρευστού.
 |
| Το μοντέλο του ιδανικού ρευστού |
Στο μοντέλο του ιδανικού ρευστού που θα κατασκευάσουμε κάνουμε τις εξής τέσσερεις υποθέσεις:
α) Ρευστό χωρίς ιξώδες.
Δηλαδή δεν λαμβάνουμε υπ'όψιν την εσωτερική τριβή.Έτσι,ένα αντικείμενο που κινείται μέσα σε ένα ρευστό το οποίο δεν έχει ιξώδες δεν υπόκειται σε καμία επιβραδύνουσα δύναμη προερχόμενη από την τριβή με το ρευστό.Θα περιοριστούμε στη μελέτη της ροής ενός ρευστού που δεν παρουσιάζει εσωτερικές τριβές και τριβές με τα τοιχώματά του σωλήνα μέσα στον οποίο ρέει
β) Στρωτή ροή.
Δηλαδή υποθέτουμε ότι κάθε σημείο του ρευστού στο χώρο έχει σταθερή ταχύτητα,δεν μεταβάλλεται με τον χρόνο.
γ) Ασυμπίεστο ρευστό.
Δηλαδή η πυκνότητα του ρευστού παραμένει σταθερή με το χρόνο.
δ) Αστρόβιλη ροή.
Η ροή ενός ρευστού είναι αστρόβιλη εάν η στροφορμή του ρευστού είναι μηδενική ως προς κάθε σημείο του.Αν δηλαδή τοποθετήσουμε έναν τροχίσκο οπουδήποτε μέσα στο ρευστό,ο τροχίσκος δεν περιστρέφεται.Εάν όμως η ροή ήταν τυρβώδης,θα υπήρχαν στρόβιλοι και ο τροχίσκος θα περιστρεφόταν.
Από τα παραπάνω μπορούμε να δώσουμε τον ορισμό του ιδανικού ρευστού.
Από τα παραπάνω μπορούμε να δώσουμε τον ορισμό του ιδανικού ρευστού.
Ιδανικό ρευστό ονοµάζεται ένα ρευστό που είναι ασυµπίεστο το οποίο ρέει χωρίς να έχει εσωτερική τριβή (ιξώδες) ούτε και συνάφεια µε τα τοιχώµατα του δοχείου
ΠΡΑΓΜΑΤΙΚΑ ΡΕΥΣΤΑ
Όμως στην πραγματικότητα η συμπεριφορά των κινούμενων ρευστών διαφέρει πολύ ή λίγο από τη συμπεριφορά των ιδανικών ρευστών.
 |
| Στην πραγματικότητα η συμπεριφορά των κινούμενων ρευστών διαφέρει πολύ ή λίγο από τη συμπεριφορά των ιδανικών ρευστών |
Έτσι για να διακρίνουμε τα υπαρκτά ρευστά από τα ιδανικά θα τα ονομάζουμε πραγματικά ρευστά.
ΡΕΥΜΑΤΙΚΗ ΓΡΑΜΜΗ
Γραµµή ροής ονοµάζεται η διαδροµή,δηλαδή η τροχιά,που ακολουθεί ένα σωµάτιο ενός κινούµενου ρευστού.
Στις συνθήκες στρωτής ροής η γραμμή ροής ονομάζεται ρευματική γραμμή.
Ρευματική γραμμή ονομάζεται η τροχιά την οποία ακολουθεί κάθε μόριο του ρευστού στη διάρκεια της κίνησής του υπό συνθήκες στρωτής ροής.
Γενικά οι ρευµατικές γραµµές δεν συµπίπτουν µε τις γραµµές ροής.Συµπίπτουν µόνο όταν η ροή είναι στρωτή και όχι όταν είναι τυρβώδης.Δηλαδή όταν η εικόνα ροής αλλάζει µε το χρόνο δεν συµπίπτουν.Τότε στην περίπτωση στρωτής ροής,η ρευµατική γραµµή είναι και η τροχιά ενός µορίου του υγρού.
Στις συνθήκες στρωτής ροής η γραμμή ροής ονομάζεται ρευματική γραμμή.
 |
| Ρευματική γραμμή ονομάζεται η τροχιά την οποία ακολουθεί κάθε μόριο του ρευστού στη διάρκεια της κίνησής του υπό συνθήκες στρωτής ροής |
.jpg) |
| Στην περίπτωση στρωτής ροής,η ρευµατική γραµµή είναι και η τροχιά ενός µορίου του υγρού |
 |
| Η ταχύτητά του μορίου του ρευστού έχει σε κάθε θέση πάντοτε τη διεύθυνση της εφαπτομένης στην ρευματική γραμμή που διέρχεται από το σημείο αυτό |
ΦΛΕΒΑ
Θεωρούμε μια επιφάνεια Α κάθετη στη διεύθυνση του σωλήνα,μέσα στον οποίο κινείται ένα ρευστό.Από κάθε σημείο του περιγράμματος της επιφάνειας Α σχεδιάζουμε την αντίστοιχη ρευματική γραμμή μέσα στο ρευστό και σχηματίζεται ένας νοητός σωλήνας που ονομάζεται φλέβα ή σωλήνας ροής.
Φλέβα ή σωλήνας ροής ονομάζεται μια ομάδα ρευματικών γραμμών.
Στη στρωτή ροή,το ρευστό δεν µπορεί να διασχίσει τα τοιχώµατα ενός σωλήνα ροής.Δηλαδή το ρευστό που κυλάει σε κάποια φλέβα δεν αναµιγνύεται µε το περιεχόµενο άλλης φλέβας του ίδιου σωλήνα.Έτσι τα γειτονικά στρώµατα π.χ νερού γλιστρούν απαλά µεταξύ τους.
Πρέπει να σημειωθεί ότι τα μόρια του ρευστού δεν μπορεί να ρέουν προς τα μέσα ή προς τα έξω των τοιχωμάτων της φλέβας,διότι τότε οι ρευματικές γραμμές θα τέμνονταν.
Φλέβα ή σωλήνας ροής ονομάζεται μια ομάδα ρευματικών γραμμών.
 |
| Φλέβα ή σωλήνας ροής ονομάζεται μια ομάδα ρευματικών γραμμών |
.jpg) |
| Σε κάθε σημείο στο περίγραμμα της επιφάνειας Α αντιστοιχεί μια ρευματική γραμμή.Όλες αυτές οι ρευματικές γραμμές ορίζουν μία φλέβα |
Ως σωλήνες θεωρούμε κάθε μορφής τοιχώματα που περιορίζουν το κινούμενο ρευστό.Για παράδειγμα σωλήνες μπορούν να θεωρηθούν η κοίτη και τα πλευρικά τοιχώματα στη ροή των ποταμών ή οι κοιλάδες στην κίνηση των ανέμων.
ΠΑΡΟΧΗ
Από μια διατομή του σωλήνα ή της φλέβας σε χρόνο Δt περνάει ένας όγκος υγρού ΔV.
Παροχή του σωλήνα ή της φλέβας ονομάζεται το πηλίκο του όγκου υγρού ΔV από μια διατομή του σωλήνα ή της φλέβας σε χρόνο Δt προς τον αντίστοιχο χρόνο αυτό.
Π=ΔV/Δt
Παροχή του σωλήνα ή της φλέβας ονομάζεται το πηλίκο του όγκου υγρού ΔV από μια διατομή του σωλήνα ή της φλέβας σε χρόνο Δt προς τον αντίστοιχο χρόνο αυτό.
Π=ΔV/Δt
όπου:
Π η παροχή του σωλήνα ή της φλέβας,
Π η παροχή του σωλήνα ή της φλέβας,
ΔV ο όγκος υγρού από μια διατομή του σωλήνα ή της φλέβας σε χρόνο Δt,
Δt ο αντίστοιχος χρόνος.
Η παροχή είναι ο όγκος ρευστού που διέρχεται από τον σωλήνα ή την φλέβα στη μονάδα του χρόνου.
Πρακτικότερα είναι δυνατή η μέτρηση της παροχής ενός υδροσωλήνα συγκεντρώνοντας το εξερχόμενο νερό σε μια δεξαμενή ή δοχείο γνωστής προηγουμένως χωρητικότητας με απλή χρονομέτρηση μέχρι της πλήρωσης αυτού.Έτσι διαιρώντας τον όγκο του νερού δια του χρόνου που διέρρευσε βρίσκεται η παροχή.
Η μονάδα μέτρησης της παροχής του σωλήνα ή της φλέβας είναι:
Η παροχή είναι ο όγκος ρευστού που διέρχεται από τον σωλήνα ή την φλέβα στη μονάδα του χρόνου.
.jpg) |
| Στο χρονικό διάστημα Δt,από μια διατομή Α του σωλήνα περνάει υγρό όγκου Α·Δx |
Η μονάδα μέτρησης της παροχής του σωλήνα ή της φλέβας είναι:
1 m3/s
Θεωρούμε ότι η διατομή του σωλήνα είναι Α και ότι το υγρό στο χρονικό διάστημα Δt έχει μετατοπιστεί κατά Δx.
Έτσι μπορούμε να γράψουμε:
ΔV=A·Δx
Έτσι μπορούμε να γράψουμε:
ΔV=A·Δx
Με απλή αντικατάσταση από τις δυο τελευταίες σχέσεις προκύπτει:
Π=Α·Δx/Δt
Π=Α·Δx/Δt
Όμως το πηλίκο Δx/Δt ισούται με την ταχύτητα υ του υγρού στη θέση αυτή,δηλαδή:
υ=Δx/Δt
Άρα έχουμε:
Π=Α·υ
υ=Δx/Δt
Άρα έχουμε:
Π=Α·υ
Συνεπώς:
Η παροχή σωλήνα ή φλέβας σε κάποια θέση είναι ίση με το γινόμενο του εμβαδού της διατομής επί την ταχύτητα του ρευστού στη θέση αυτή.
ΔV1=A1·Δx1=A1·υ1·Δt
Δx2=υ2·Δt
ΔV2=A2·Δx2=A2·υ2·Δt
Όμως το ρευστό θεωρείται ασυμπίεστο που σημαίνει ότι η πυκνότητα του είναι ίδια σε όλη την έκταση του.
Γνωρίζουμε όμως ότι η μάζα διατηρείται και επειδή έχουμε στρωτή ροή,θα πρέπει η μάζα Δm1 που περνάει από τη διατομή Α1 του σωλήνα στο χρονικό διάστημα Δt να είναι ίση με τη μάζα Δm2 που περνάει από μία άλλη διατομή του σωλήνα Α2 στο ίδιο χρονικό διάστημα Δt.
Δm1=Δm2 ή
ρ·ΔV1=ρ·ΔV2 ή
ρ·A1·υ1·Δt=ρ·A2·υ2·Δt ή
και τελικά:
A1·υ1=A2·υ2
Η εξίσωση αυτή ονομάζεται εξίσωση της συνέχειας.
Η εξίσωση της συνέχειας ισοδυναμεί με το γεγονός ότι η ποσότητα που εισέρχεται στον σωλήνα στο χρονικό διάστημα Δt είναι ίση με την ποσότητα που εξέρχεται από τον σωλήνα στο ίδιο χρονικό διάστημα.
Η παροχή σωλήνα ή φλέβας σε κάποια θέση είναι ίση με το γινόμενο του εμβαδού της διατομής επί την ταχύτητα του ρευστού στη θέση αυτή.
ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ
ΕΙΣΑΓΩΓΗ
Ο Νόμος της συνέχειας της ροής είναι από τους σημαντικότερους νόμους στην Υδροδυναμική.
Η σχέση που περιγράφει αυτόν τον νόμο ονομάζεται εξίσωση της συνέχειας της ροής και είναι άμεση συνέπεια της αρχής διατήρησης της ύλης.
Η αρχή αυτή προέρχεται από το γεγονός ότι η μάζα διατηρείται πάντα σε υγρά συστήματα ανεξάρτητα από την πολυπλοκότητα του αγωγού ή την κατεύθυνση της ροής.
Αναφέρει ότι η παροχή παραμένει σταθερή κατά μήκος μίας φλέβας ή ενός σωλήνα,που διαρρέεται από υγρό.
Η σχέση που περιγράφει αυτόν τον νόμο ονομάζεται εξίσωση της συνέχειας της ροής και είναι άμεση συνέπεια της αρχής διατήρησης της ύλης.
 |
| Η παροχή παραμένει σταθερή κατά μήκος μίας φλέβας (ενός σωλήνα),που διαρρέεται από υγρό |
Αναφέρει ότι η παροχή παραμένει σταθερή κατά μήκος μίας φλέβας ή ενός σωλήνα,που διαρρέεται από υγρό.
ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ
Θεωρούμε ότι η ροή ενός ρευστού γίνεται σ' ένα σωλήνα μεταβλητής διατομής.Τα μόρια του ρευστού κινούνται παράλληλα από τις δυναμικές γραμμές υπό συνθήκες στρωτής ροής.
Σε όλα τα σημεία οι ταχύτητες των μορίων εφάπτονται των αντίστοιχων ρευματικών γραμμών τις οποίες ακολουθούν.
Θεωρούμε ότι η ροή ενός ρευστού γίνεται σ' ένα σωλήνα μεταβλητής διατομής.Τα μόρια του ρευστού κινούνται παράλληλα από τις δυναμικές γραμμές υπό συνθήκες στρωτής ροής.
Σε όλα τα σημεία οι ταχύτητες των μορίων εφάπτονται των αντίστοιχων ρευματικών γραμμών τις οποίες ακολουθούν.
 |
| Θεωρούμε ότι η ροή ενός ρευστού γίνεται σ' ένα σωλήνα μεταβλητής διατομής |
Θεωρούμε ένα ασυμπίεστο ρευστό που ρέει μέσα στο σωλήνα της μεταβλητής διατομής.
Στο μικρό χρονικό διάστημα Δt το ρευστό στο αριστερό μέρος του σωλήνα κινείται διανύοντας απόσταση:
Δx1=υ1·Δt
όπου:
Δx1 η απόσταση που διανύει το ρευστό στο αριστερό μέρος του σωλήνα,στο μικρό χρονικό διάστημα Δt,
υ1 η ταχύτητα του ρευστού στην διατομή Α1,
Δt το μικρό χρονικό διάστημα.
 |
| Στο μικρό χρονικό διάστημα Δt το ρευστό στο αριστερό μέρος του σωλήνα κινείται διανύοντας απόσταση Δx1=υ1·Δt |
Αν ΔV1 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm1 και Α1 η διατομή του σωλήνα στην περιοχή αυτήν,τότε η μάζα που ρέει στην ίδια περιοχή είναι:
Δm1=ρ·ΔV1
όπου:
Δm1 η στοιχειώδης μάζα που ρέει στην ίδια περιοχή στο αριστερό μέρος του σωλήνα,
ρ η πυκνότητα του ρευστού,
ΔV1 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm1.
Όμως:
ΔV1=A1·Δx1=A1·υ1·Δt
΄ Άρα:
Δm1=ρ·ΔV1=ρ·Α1·Δx1=ρ·Α1·υ1·Δt
Παρομοίως στο ίδιο μικρό χρονικό διάστημα Δt το ρευστό στο δεξιό μέρος του σωλήνα κινείται διανύοντας απόσταση:
όπου:
Δx2 η απόσταση που διανύει το ρευστό στο αριστερό μέρος του σωλήνα,στο μικρό χρονικό διάστημα Δt,
υ2 η ταχύτητα του ρευστού στην διατομή Α1,
Δt το μικρό χρονικό διάστημα.
 |
| Σε σημεία όπου ο σωλήνας στενεύει η ταχύτητα ροής είναι πιο μεγάλη |
Αν ΔV2 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm2 και Α2 η διατομή του σωλήνα στην περιοχή αυτήν,τότε η μάζα που ρέει στην ίδια περιοχή είναι:
Δm2=ρ·ΔV2
όπου:
Δm2 η στοιχειώδης μάζα που ρέει στην ίδια περιοχή στο δεξιό μέρος του σωλήνα,
ρ η πυκνότητα του ρευστού,
ΔV2 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm2.
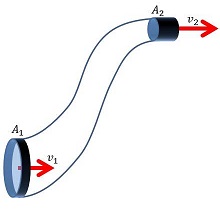 |
| Το μέτρο της ταχύτητας του ρευστού είναι μεγάλο εκεί όπου ο σωλήνας είναι στενός και μικρό εκεί όπου ο σωλήνας είναι φαρδύς |
Όμως:
ΔV2=A2·Δx2=A2·υ2·Δt
΄ Άρα:
Δm2=ρ·ΔV2=ρ·Α2·Δx2=ρ·Α2·υ2·Δt
Όμως το ρευστό θεωρείται ασυμπίεστο που σημαίνει ότι η πυκνότητα του είναι ίδια σε όλη την έκταση του.
 |
| Η ποσότητα που εισέρχεται στον σωλήνα στο χρονικό διάστημα Δt είναι ίση με την ποσότητα που εξέρχεται από τον σωλήνα στο ίδιο χρονικό διάστημα |
Είναι:
Δm1=Δm2 ή
ρ·ΔV1=ρ·ΔV2 ή
ρ·Α1·Δx1=ρ·Α2·Δx2 ή
ρ·A1·υ1·Δt=ρ·A2·υ2·Δt ή
και τελικά:
A1·υ1=A2·υ2
Η εξίσωση αυτή ονομάζεται εξίσωση της συνέχειας.
.jpg) |
| Η εξίσωση A1·υ1=A2·υ2 ονομάζεται εξίσωση της συνέχειας και είναι άμεση συνέπεια της αρχής διατήρησης της ύλης |
Άρα η εξίσωση της συνέχειας διατυπώνεται ως εξής:
Για όλα τα σημεία ενός σωλήνα ή μιας φλέβας το γινόμενο της επιφάνειας διατομής επί την ταχύτητα του ρευστού είναι σταθερό.
Άρα το μέτρο της ταχύτητας του ρευστού είναι μεγάλο εκεί όπου ο σωλήνας είναι στενός και μικρό εκεί όπου ο σωλήνας είναι φαρδύς.
 |
| Για όλα τα σημεία του σωλήνα ή της φλέβας το γινόμενο της επιφάνειας διατομής επί την ταχύτητα του ρευστού είναι σταθερό |
Η εξίσωση της συνέχειας είναι άμεση συνέπεια της αρχής διατήρησης της ύλης.
 |
| Η εξίσωση της συνέχειας είναι άμεση συνέπεια της αρχής διατήρησης της ύλης |
ΝΟΜΟΣ ΣΥΝΕΧΕΙΑΣ
Η παροχή σωλήνα ή φλέβας σε κάποια θέση είναι ίση με το γινόμενο του εμβαδού της διατομής επί την ταχύτητα του ρευστού στη θέση αυτή.
Π=Α·υ
Άρα η εξίσωση της συνέχειας γράφεται και:
Π=Α·υ
Άρα η εξίσωση της συνέχειας γράφεται και:
Π1=Π2 ή
Π=σταθερό
Π=σταθερό
Η σχέση Π=σταθερό ισχύει για σωλήνα αλλά και για φλέβα και διατυπώνεται ως εξής:
Κατά μήκος ενός σωλήνα ή μιας φλέβας η παροχή διατηρείται σταθερή.
Η διατύπωση αυτή ονομάζεται Νόμος της συνέχειας της ροής.
Ο Νόμος της συνέχειας της ροής είναι από τους σημαντικότερους νόμους στην Υδροδυναμική.
 |
| Κατά μήκος ενός σωλήνα ή μιας φλέβας η παροχή διατηρείται σταθερή |
Από τη σχέση A1·υ1=A2·υ2 φαίνεται ότι κατά μήκος ενός σωλήνα που δεν έχει σταθερή διατομή,η ταχύτητα του υγρού δεν είναι παντού ίδια.Σε σημεία όπου ο σωλήνας στενεύει η ταχύτητα ροής είναι πιο μεγάλη.
.jpg) |
| Η ταχύτητα ροής είναι μεγαλύτερη εκεί που πυκνώνουν οι ρευματικές γραμμές |
Κατά μήκος ενός ποταμού με σταθερό πλάτος πολλές φορές το βάθος ποικίλει.Όπου το ποτάμι έχει μικρό βάθος έχει και μικρή εγκάρσια διατομή.
 |
| Επειδή η παροχή είναι σταθερή,στις περιοχές όπου το ποτάμι είναι ρηχό το νερό κυλάει γρηγορότερα |
Επειδή η παροχή είναι σταθερή,στις περιοχές όπου το ποτάμι είναι ρηχό το νερό κυλάει γρηγορότερα.Μπορούμε να πούμε ότι εκεί που οι ρευματικές γραμμές πυκνώνουν η ταχύτητα ροής είναι πιο μεγάλη.
W=W1-W2=p1·A1·Δs1-p2·A2·Δs2=(p1-p2)·ΔV
Η παραπάνω σχέση είναι η εξίσωση του Bernoulli για ένα ασυμπίεστο ρευστό,χωρίς ιξώδες και για συνθήκες στρωτής ροής.
p+1/2·ρ·υ2=σταθερό
ΑΡΧΗ BERNOULLI
Κατά τη ροή του υγρού,η πίεση είναι μικρή στα σημεία όπου η ταχύτητα είναι μεγάλη,και αντίστροφα είναι μεγάλη σε σημεία όπου η ταχύτητα είναι μικρή.
ή ακόμα,
Το άθροισμα της "ενέργειας θέσεως" και της "κινητικής ενέργειας" είναι σταθερό.
Τούτο άλλωστε γίνεται εύκολα αντιληπτό δεδομένου ότι όταν αυξάνεται η κινητική ενέργεια του υγρού,η αύξηση αυτή πραγματοποιείται με αντίστοιχη ελάττωση της ενέργειας θέσεως προκειμένου το άθροισμα τους να παραμένει σταθερό.
Η πίεση στο πρώτο σωλήνα μέτρησης (1) είναι υψηλότερη από ότι στο δεύτερο,και η ταχύτητα του υγρού στο (1) είναι μικρότερη από ότι στο (2),επειδή η περιοχή της εγκάρσιας τομής στο (1) είναι μεγαλύτερη από ότι στο (2).
Εφαρμόζοντας την εξίσωση του Bernoulli στα σημεία 1 και 2 που βρίσκονται στο ίδιο ύψος έχουμε:
p1+1/2·ρ·υ12=p2+1/2·ρ·υ22
Από τις δυο εξισώσεις με απλή αντικατάσταση έχουμε:
p1+1/2·ρ·υ12=p2+1/2·ρ· A12/A22 · υ12 ή
p1-p2=1/2·ρ·υ12·(A1/A2-1)
Όμως:
p1=pαtm+ρ·g·h1
και
p2=pαtm+ρ·g·h2
όπου:
ΕΞΙΣΩΣΗ BERNOULLI (ΜΠΕΡΝΟΥΛΙ)
 |
| ΕΞΙΣΩΣΗ BERNOULLI (ΜΠΕΡΝΟΥΛΙ) |
ΕΙΣΑΓΩΓΗ
Από την καθημερινότητα μας ξέρουμε ότι η πίεση ενός ρευστού που ρέει μέσα σε ένα σωλήνα είναι διαφορετική ανάμεσα σε δύο σημεία που έχουν υψομετρική διαφορά.Για παράδειγμα το νερό στις βρύσες του τρίτου ορόφου έχει μικρότερη πίεση από το νερό στις βρύσες του ισογείου.
Από την εξίσωση της συνέχειας γνωρίζουμε ότι σε έναν σωλήνα μεταβλητής διατομής,η ταχύτητα του υγρού μεταβάλλεται.Έτσι μια μικρή μάζα A·m του υγρού σε άλλες περιοχές του σωλήνα επιταχύνεται και σε άλλες επιβραδύνεται.Η συνολική δύναμη που δέχεται αυτή η μάζα από το περιβάλλον υγρό δεν είναι μηδενική και άρα η πίεση μεταβάλλεται σε όλες τις περιοχές του σωλήνα.
 |
| Hydrodynamica (1738) |
Το 1738 με την δημοσίευση του βιβλίου του Hydrodynamica ο Ελβετός Daniel Bernoulli επινόησε μια σχέση η οποία συνδέει την πίεση με την ταχύτητα του ρευστού και με το ύψος.
Όπως θα δούμε,η σχέση αυτή είναι άμεσο αποτέλεσμα της εφαρμογής της διατήρησης της ενέργειας σε ένα ιδανικό ρευστό.
Όπως θα δούμε,η σχέση αυτή είναι άμεσο αποτέλεσμα της εφαρμογής της διατήρησης της ενέργειας σε ένα ιδανικό ρευστό.
ΕΞΙΣΩΣΗ BERNOULLI
Θα θεωρήσουμε ότι το ρευστό είναι ασυμπίεστο,χωρίς ιξώδες και ότι ρέει χωρίς στροβίλους,με στρωτή ροή.Θεωρούμε ότι η ροή γίνεται στο χρονικό διάστημα Δt μέσα σε έναν σωλήνα μεταβλητής διατομής,όπως φαίνεται στο παρακάτω σχήμα.
Θα μελετήσουμε την πίεση σε δύο σημεία Β,Γ,του σωλήνα.Το σημείο Β βρίσκεται σε ύψος y1 από το έδαφος και ο σωλήνας έχει στην περιοχή του Β διατομή Α1.
Θα μελετήσουμε την πίεση σε δύο σημεία Β,Γ,του σωλήνα.Το σημείο Β βρίσκεται σε ύψος y1 από το έδαφος και ο σωλήνας έχει στην περιοχή του Β διατομή Α1.
.jpg) |
| Έστω ότι έχουμε ένα σωλήνα μεταβλητής διατομής μέσα στον οποίο ρέει ένα ασυμπίεστο ρευστό. Θα εξετάσουμε την πίεση σε δύο σημεία του σωλήνα |
Εάν η πίεση του ρευστού στο Β,που είναι το χαμηλότερο σημείο της ροής,είναι p1,τότε η δύναμη είναι:
F1=p1·Α1
Το σημείο Γ βρίσκεται σε ύψος y2 από το έδαφος και ο σωλήνας έχει στην περιοχή του Γ διατομή Α2.Εάν η πίεση του ρευστού στο Γ,που είναι το υψηλότερο σημείο της ροής,είναι p2,τότε η δύναμη είναι:
F2=p2·Α2
Η δύναμη αυτή έχει φορά αντίθετη από τη φορά της δύναμης F1=p1·A1.
Στο πολύ μικρό χρονικό διάστημα Δt ένα στοιχειώδες τμήμα του ρευστού στην περιοχή του Β μετατοπίζεται κατά Δs1 ενώ ένα αντίστοιχο τμήμα του ρευστού ίσης μάζας,άρα και όγκου,στην περιοχή του Γ μετατοπίζεται κατά Δs2.
Το έργο που παράγει η δύναμη F1 στο κάτω μέρος του ρευστού κατά το πολύ μικρό χρονικό διάστημα Δt είναι:
W1=F1·Δs1=p1·Α1·Δs1
Παρομοίως,το έργο που παράγει η δύναμη F2 στο πάνω μέρος του ρευστού κατά το πολύ μικρό χρονικό διάστημα Δt είναι:
W2=-F2·Δs2=- p2·Α2·Δs2
F1=p1·Α1
Το σημείο Γ βρίσκεται σε ύψος y2 από το έδαφος και ο σωλήνας έχει στην περιοχή του Γ διατομή Α2.Εάν η πίεση του ρευστού στο Γ,που είναι το υψηλότερο σημείο της ροής,είναι p2,τότε η δύναμη είναι:
F2=p2·Α2
Η δύναμη αυτή έχει φορά αντίθετη από τη φορά της δύναμης F1=p1·A1.
 |
| Η δύναμη F2 έχει φορά αντίθετη από τη φορά της δύναμης F1 |
Το έργο που παράγει η δύναμη F1 στο κάτω μέρος του ρευστού κατά το πολύ μικρό χρονικό διάστημα Δt είναι:
W1=F1·Δs1=p1·Α1·Δs1
Παρομοίως,το έργο που παράγει η δύναμη F2 στο πάνω μέρος του ρευστού κατά το πολύ μικρό χρονικό διάστημα Δt είναι:
W2=-F2·Δs2=- p2·Α2·Δs2
Το έργο είναι αρνητικό,διότι η δύναμη του ρευστού εναντιώνεται στη μετατόπιση.Όμως ο όγκος του ρευστού που περνάει από την περιοχή 1 κατά το πολύ μικρό χρονικό διάστημα Δt είναι ίσος με τον όγκο του ρευστού που περνάει από την περιοχή 2 κατά το ίδιο μικρό χρονικό διάστημα Δt.
Έτσι,το συνολικό έργο που παράγουν οι δυνάμεις αυτές κατά το πολύ μικρό χρονικό διάστημα Δt είναι άθροισμα του έργου της δύναμης F1=p1·Α1 (θετικό) συν του έργου της δύναμης F2=p2·Α2 (αρνητικό):
W=W1-W2=p1·A1·Δs1-p2·A2·Δs2
Όμως ο όγκος του ρευστού που περνάει από την περιοχή 1 κατά το πολύ μικρό χρονικό διάστημα Δt είναι ίσος με τον όγκο του ρευστού που περνάει από την περιοχή 2 κατά το ίδιο μικρό χρονικό διάστημα Δt.
 |
| Στο στενό μέρος του σωλήνα η ταχύτητα του υγρού είναι μεγαλύτερη |
Άρα:
A1·Δs1=A2·Δs2=ΔV
Οπότε:
W=W1-W2=p1·A1·Δs1-p2·A2·Δs2=(p1-p2)·ΔV
Μέρος του έργου αυτού μεταβάλλει την κινητική ενέργεια του ρευστού και άλλο μέρος μεταβάλλει τη βαρυτική δυναμική ενέργεια του.Εάν Δm είναι η ποσότητα μάζας που περνάει από τον σωλήνα στο χρονικό διάστημα Δt,τότε η μεταβολή της κινητικής ενέργειας είναι:
ΔΚ=1/2·Δm·υ22-1/2·Δm·υ21=1/2·ρ·ΔV·(υ22-υ21)
όπου:
υ1 η ταχύτητα του ρευστού στο Β και
υ2 η ταχύτητα του ρευστού στο Γ.
υ1 η ταχύτητα του ρευστού στο Β και
υ2 η ταχύτητα του ρευστού στο Γ.
Η μεταβολή της δυναμικής ενέργεια είναι:
ΔU=Δm·g·y2-Δm·g·y1
καθώς,στην ουσία,ένα τμήμα του ρευστού A·m έφυγε από το ύψος y1 και βρέθηκε στο ύψος y2.
ΔU=Δm·g·y2-Δm·g·y1
Το έργο του βάρους στο ίδιο χρονικό διάστημα Δt είναι:
WB=-ΔU=-(Δm·g·y2-Δm·g·y1)=-Δm·g·(y2-y1)=-ρ·ΔV·g·(y2-y1)
καθώς,στην ουσία,ένα τμήμα του ρευστού A·m έφυγε από το ύψος y1 και βρέθηκε στο ύψος y2.
.jpg) |
| Στο στενό μέρος του σωλήνα η ταχύτητα του υγρού είναι μεγαλύτερη.Το ύψος της στάθμης του υγρού πάνω από την περιοχή αυτή δείχνει ότι η πίεση στο σωλήνα είναι μικρότερη |
Μπορούμε να εφαρμόσουμε το θεώρημα έργου-ενέργειας για αυτόν τον όγκο ρευστού στο μικρό χρονικό διάστημα Δt.
Έχουμε:
Έχουμε:
ΣW=ΔΚ
W+WB=ΔΚ
όπου:
W το συνολικό έργο που παράγουν οι δυνάμεις αυτές κατά το πολύ μικρό χρονικό διάστημα Δt.
W το συνολικό έργο που παράγουν οι δυνάμεις αυτές κατά το πολύ μικρό χρονικό διάστημα Δt.
.jpg) |
| Η εξίσωση του Bernoulli αποτελεί έκφραση της αρχής διατήρησης της ενέργειας στη ροή των ρευστών |
Αντικαθιστώντας τις σχέσεις αυτές έχουμε:
W+WB=ΔΚ
(p1-p2)·ΔV-ρ·ΔV·g·(y2-y1)=1/2·ρ·ΔV·(υ22-υ21)
W+WB=ΔΚ
(p1-p2)·ΔV-ρ·ΔV·g·(y2-y1)=1/2·ρ·ΔV·(υ22-υ21)
Διαιρούμε κάθε όρο με ΔV,αντικαθιστούμε ρ=Δm/ΔV και βρίσκουμε:
p1+1/2·ρ·υ21+ρ·g·y1=p2 +1/2·ρ·υ22+ρ·g·y2
Η σχέση αυτή ισχύει για οποιοδήποτε ζεύγος σημείων άρα μπορεί να γραφτεί και με τη μορφή:
p+1/2·ρ·υ2+ρ·g·y=σταθερό
p+1/2·ρ·υ2+ρ·g·y=σταθερό
Η παραπάνω σχέση είναι η εξίσωση του Bernoulli για ένα ασυμπίεστο ρευστό,χωρίς ιξώδες και για συνθήκες στρωτής ροής.
Όταν το ρευστό είναι ακίνητο,υ1=υ2=0 και y2-y1=h τότε η εξίσωση του Bernoulli γίνεται:
p1-p2=ρ·g·y2
Αν ο σωλήνας είναι οριζόντιος η εξίσωση του Bernoulli παίρνει τη μορφή:
Αν ο σωλήνας είναι οριζόντιος η εξίσωση του Bernoulli παίρνει τη μορφή:
p+1/2·ρ·υ2=σταθερό
από όπου φαίνεται ότι σε περιοχές όπου πυκνώνουν οι ρευματικές γραμμές (μικρή διατομή του σωλήνα) και η ταχύτητα ροής αυξάνεται,η πίεση ελαττώνεται.
ΑΡΧΗ BERNOULLI
Από την εξίσωση του Bernoulli προκύπτει ότι:
Το άθροισμα της πίεσης (p),της κινητικής ενέργειας ανά μονάδα όγκου (1/2·ρ·υ2) και της δυναμικής ενέργειας ανά μονάδα όγκου (ρ·g·y) έχει την ίδια σταθερή τιμή σε οποιοδήποτε σημείο της ρευματικής γραμμής.
Το άθροισμα της πίεσης (p),της κινητικής ενέργειας ανά μονάδα όγκου (1/2·ρ·υ2) και της δυναμικής ενέργειας ανά μονάδα όγκου (ρ·g·y) έχει την ίδια σταθερή τιμή σε οποιοδήποτε σημείο της ρευματικής γραμμής.
Η διατύπωση αυτή ονομάζεται αρχή του Bernoulli ή καλούμενο και Θεμελιώδες θεώρημα της Υδροδυναμικής η οποία αποτελεί έκφραση της αρχής διατήρησης της ενέργειας στη ροή των ρευστών.
Στη πραγματικότητα πρόκειται για ένα άθροισμα τριών ενεργειών:της "ενέργειας θέσεως",της "δυναμικής πίεσης",που αποτελεί το μέτρο της "κινητικής ενέργειας" του υγρού,και της "υδροστατικής πίεσης",που είναι και το μέτρο της "δυναμικής ενέργειας" λόγω ύψους ή λόγω του πεδίου βαρύτητας.
Κατόπιν όλων των παραπάνω,ως κατάληξη,ο Νόμος του Μπερνούλι καθορίζει ότι:
Κατά μήκος μιας φλέβας ή ενός αγωγού που διέρχεται υγρό το άθροισμα της εξωτερικής πίεσης,της δυναμικής πίεσης και της υδροστατικής πίεσης είναι σταθερό.
Εξ αυτού του τελευταίου συνάγεται ότι:
Κατά μήκος μιας φλέβας ή ενός αγωγού που διέρχεται υγρό το άθροισμα της εξωτερικής πίεσης,της δυναμικής πίεσης και της υδροστατικής πίεσης είναι σταθερό.
Εξ αυτού του τελευταίου συνάγεται ότι:
Κατά τη ροή του υγρού,η πίεση είναι μικρή στα σημεία όπου η ταχύτητα είναι μεγάλη,και αντίστροφα είναι μεγάλη σε σημεία όπου η ταχύτητα είναι μικρή.
ή ακόμα,
Το άθροισμα της "ενέργειας θέσεως" και της "κινητικής ενέργειας" είναι σταθερό.
Τούτο άλλωστε γίνεται εύκολα αντιληπτό δεδομένου ότι όταν αυξάνεται η κινητική ενέργεια του υγρού,η αύξηση αυτή πραγματοποιείται με αντίστοιχη ελάττωση της ενέργειας θέσεως προκειμένου το άθροισμα τους να παραμένει σταθερό.
ΘΕΩΡΗΜΑ TORRICELLI (ΤΟΡΙΚΕΛΙ)
Εφαρμόζουμε το νόμο του Bernoulli για τις θέσεις Ε (ελεύθερη επιφάνεια) και Κ (στόμιο εκροής):
pE+1/2·ρ·υΕ2+ρ·g·h=pK+1/2·ρ·υK2+0
pE=pK=pαt
Η ταχύτητα με την οποία κατεβαίνει η στάθμη του υγρού μπορεί να θεωρηθεί αμελητέα συγκριτικά με την ταχύτητα με την οποία ρέει το νερό στο Κ:
υE=0
ΧΡΟΝΟΣ ΓΙΑ ΝΑ ΑΔΕΙΑΣΕΙ ΤΟ ΔΟΧΕΙΟ
Έχουμε:
Α·dh=α·dx
όπου:
Α το εμβαδόν της ελεύθερης επιφάνειας,
α το εμβαδόν της διατομής εκροής,
dh το ύψος του υγρού στο δοχείο,
dx το μήκος του σωληνάριου σε χρόνο dt.



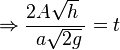

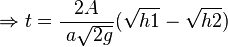
είναι ο χρόνος που απαιτείται για να αδειάσει το νερό δοχείου από το ύψος h1 μέχρι το ύψος h2.
 |
| ΘΕΩΡΗΜΑ TORRICELLI (ΤΟΡΙΚΕΛΙ) |
ΕΙΣΑΓΩΓΗ
Το Θεώρημα του Τοριτσέλι προσδιορίζει την εκροή ιδεώδους ρευστού στο ελεύθερο αέρα.Προϋπόθεση ισχύος του θεωρήματος αυτού είναι το εμβαδόν διατομής εκροής να είναι κατά πολύ μικρότερο της ελεύθερης επιφάνειας.
Ο νόμος ανακαλύφθηκε (αν και όχι σε αυτή τη μορφή) από την Ιταλό επιστήμονα Evangelista Torricelli,το 1644.Αργότερα αποδείχθηκε ότι είναι μια ειδική περίπτωση της αρχής του Bernoulli.
ΜΑΘΗΜΑΤΙΚΗ ΕΚΦΡΑΣΗ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ ΤΟΥ TORRICELLI
Θεωρούμε το δοχείο του παρακάτω σχήματος στη βάση του οποίου υπάρχει στόμιο εκροής.Θα υπολογίσουμε την ταχύτητας εκροής υγρού του ανοικτού δοχείου.
ΜΑΘΗΜΑΤΙΚΗ ΕΚΦΡΑΣΗ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ ΤΟΥ TORRICELLI
Θεωρούμε το δοχείο του παρακάτω σχήματος στη βάση του οποίου υπάρχει στόμιο εκροής.Θα υπολογίσουμε την ταχύτητας εκροής υγρού του ανοικτού δοχείου.
.jpg) |
| Θεωρούμε το δοχείο στη βάση του οποίου υπάρχει στόμιο εκροής.Θέλουμε να υπολογίσουμε την ταχύτητας εκροής υγρού του ανοικτού δοχείου |
pE+1/2·ρ·υΕ2+ρ·g·h=pK+1/2·ρ·υK2+0
Η πίεση τόσο στην ελεύθερη επιφάνεια όσο και στο σημείο εξόδου είναι η ατμοσφαιρική,δηλαδή:
pE=pK=pαt
Η ταχύτητα με την οποία κατεβαίνει η στάθμη του υγρού μπορεί να θεωρηθεί αμελητέα συγκριτικά με την ταχύτητα με την οποία ρέει το νερό στο Κ:
Λαμβάνοντας υπόψη τις δυο τελευταίες σχέσεις και επιλύοντας την πρώτη ως προς υκ βρίσκουμε:
που αποτελεί τη μαθηματική έκφραση του θεωρήματος του Torricelli (Τορικέλι) που το διατύπωσε το 1644 ο Evangelista Torricelli.
 |
| Το θεώρημα του Torricelli (Τορικέλι) |
Την ίδια χρονιά ο Evangelista Torricelli ανακάλυψε το υδραργυρικό βαρόμετρο.
ΔΙΑΤΥΠΩΣΗ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ ΤΟΥ TORRICELLI
Το θεώρημα του Torricelli (Τορικέλι) διατυπώνεται ως εξής:
Το θεώρημα του Torricelli (Τορικέλι) διατυπώνεται ως εξής:
Η ταχύτητα εκροής υγρού από στόμιο που βρίσκεται σε βάθος h από την ελεύθερη επιφάνειά του είναι ίση με την ταχύτητα που θα είχε το υγρό αν έπεφτε ελεύθερα από ύψος h.
.jpg) |
| Η ταχύτητα εκροής υγρού από στόμιο που βρίσκεται σε βάθος h από την ελεύθερη επιφάνειά του είναι ίση με την ταχύτητα που θα είχε το υγρό αν έπεφτε ελεύθερα από ύψος h |
Αργότερα αποδείχθηκε ότι είναι μια ειδική περίπτωση της αρχής του Bernoulli.
Θεωρούμε να δοχείο που περιέχει νερό και αδειάζει ελεύθερα μέσω ενός σωλήνα.Έστω h το ύψος του νερού σε οποιαδήποτε στιγμή.
 |
| Θεωρούμε να δοχείο που περιέχει νερό και αδειάζει ελεύθερα μέσω ενός σωλήνα.Έστω h το ύψος του νερού σε οποιαδήποτε στιγμή |
Η ταχύτητα εκροής είναι:
Έχουμε:
Α·dh=α·dx
όπου:
Α το εμβαδόν της ελεύθερης επιφάνειας,
α το εμβαδόν της διατομής εκροής,
dh το ύψος του υγρού στο δοχείο,
dx το μήκος του σωληνάριου σε χρόνο dt.



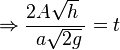

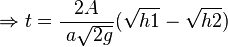
είναι ο χρόνος που απαιτείται για να αδειάσει το νερό δοχείου από το ύψος h1 μέχρι το ύψος h2.
ΡΟΟΜΕΤΡΟ ΤΟΥ VENTURI (ΒΕΝΤΟΥΡΙ)
.jpg) |
| ΡΟΟΜΕΤΡΟ ΤΟΥ VENTURI (ΒΕΝΤΟΥΡΙ) |
ΕΙΣΑΓΩΓΗ
Το ροόμετρο του Ventouri είναι μία διάταξη που χρησιμεύει για τη μέτρηση της ταχύτητας ροής σε ένα σωλήνα.
Η διάταξή αυτή λειτουργεί πάνω στο φαινόμενο Venturi που περιγράφει τη μείωση στην πίεση του ρευστού που προκύπτει όταν ένα ρευστό ρέει μέσω ενός περιορισμένου τμήματος του σωλήνα.
Το φαινόμενο Venturi πήρε το όνομά του από Giovanni Battista Venturi (1746-1822),ένα Ιταλό φυσικό.
ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΧΥΤΗΤΑΣ ΡΟΗΣ
Το ροόμετρο του Ventouri είναι μία διάταξη που χρησιμεύει για τη μέτρηση της ταχύτητας ροής σε ένα σωλήνα.
.jpg) |
| Το ροόμετρο του Ventouri είναι μία διάταξη που χρησιμεύει για τη μέτρηση της ταχύτητας ροής σε ένα σωλήνα |
.jpg) |
| Ο Giovanni Battista Venturi (15, Μαρτίου, 1746 - 24 Απριλίου 1822) ήταν Ιταλός φυσικός , σοφός,άνθρωπος των γραμμάτων, διπλωμάτης και ιστορικός της επιστήμης.Ανακάλυψε το φαινόμενο Venturi το 1797 |
ΥΠΟΛΟΓΙΣΜΟΣ ΤΑΧΥΤΗΤΑΣ ΡΟΗΣ
Θεωρούμε τις διατομές Α1 και Α2,του σωλήνα και τη υψομετρική διαφορά h στη στάθμη των δύο κατακόρυφων ανοιχτών σωλήνων Β και Γ.
Θέλουμε να βρούμε τη ταχύτητα ροής στην περιοχή του σωλήνα που έχει διατομή Α1.
Θέλουμε να βρούμε τη ταχύτητα ροής στην περιοχή του σωλήνα που έχει διατομή Α1.
.jpg) |
| Θεωρούμε τις διατομές Α1 και Α2,του σωλήνα και τη υψομετρική διαφορά h στη στάθμη των δύο κατακόρυφων ανοιχτών σωλήνων Β και Γ |
Εφαρμόζοντας την εξίσωση του Bernoulli στα σημεία 1 και 2 που βρίσκονται στο ίδιο ύψος έχουμε:
Από την εξίσωση της συνέχειας έχουμε ότι:
A1·υ1=A2·υ2 ή
υ2=A1/A2 · υ1
A1·υ1=A2·υ2 ή
υ2=A1/A2 · υ1
Από τις δυο εξισώσεις με απλή αντικατάσταση έχουμε:
p1+1/2·ρ·υ12=p2+1/2·ρ· A12/A22 · υ12 ή
p1-p2=1/2·ρ·υ12·(A1/A2-1)
Όμως:
p1=pαtm+ρ·g·h1
και
p2=pαtm+ρ·g·h2
όπου:
h1 το ύψος της στήλης του νερού πάνω από το σωλήνα μετρημένο από το σημείο 1 και
h2 το ύψος της στήλης του νερού μετρημένο από το σημείο 2.
.jpg) |
| Ένας άλλος τύπος του ροομέτρου του Ventouri |
Αφαιρώντας κατά μέλη τις δυο τελευταίες σχέσεις παίρνουμε:
p1-p2=ρ·g·(h1-h2)=ρ·g·h
Αντικαθιστώντας στην p1-p2=1/2·ρ·υ12·(A1/A2-1) την p1-p2=ρ·g·(h1-h2)=ρ·g·h βρίσκουμε:
ρ·g·h=1/2·ρ·υ12·(A12/A22-1)
και τελικά:
και τελικά:
υ1=[2·g·h/(A1/A2 )2-1]1/2
Τα ρευστά δεν αντέχουν σε διατμητικές παραμορφώσεις.Πάντως τα ρευστά αντιστέκονται σε μικρό βαθμό στη διατμητική κίνηση.Αυτή η αντίσταση στην κίνηση στρωμάτων του ρευστού είναι ένα είδος εσωτερικής τριβής,που ονομάζεται ιξώδες.Στην περίπτωση των υγρών το ιξώδες οφείλεται στη δύναμη τριβής ανάμεσα σε παρακείμενα στρώματα του ρευστού καθώς αυτά ολισθαίνουν το ένα πάνω στο άλλο.
Στη μηχανική των ρευστών διατμητική τάση ονομάζεται η δύναμη που συνηθέστερα παραμορφώνει τα ρευστά στη ροή τους,ανεξάρτητα το πόσο μικρή μπορεί να είναι.
Το ιξώδες μετριέται με ειδικό όργανο που λέγεται ιξωδόμετρο.
Η μονάδα μέτρησης του συντελεστή ιξώδους στο S.I. είναι:
1 Ν·s/m2
Νευτώνεια ρευστά ονομάζονται τα ρευστά που υπακούουν στην εξίσωση n=F·l/Α·υ.
Χαρακτηρίζονται όσα εμφανίζουν τις αποτρεπτικές ιδιότητες των προηγουμένων π.χ. το νερό,υδατικά διαλύματα,ορισμένοι υδατικοί διαλύτες,τα αραιά αιωρήματα και γαλακτώματα,καθώς και όλα τα αέρια.
ΤΡΙΒΗ ΣΤΑ ΡΕΥΣΤΑ
 |
| ΤΡΙΒΗ ΣΤΑ ΡΕΥΣΤΑ |
ΕΙΣΑΓΩΓΗ
Έχουμε θεωρήσει μέχρι στιγμής ότι τα ρευστά ρέουν χωρίς να αναπτύσσονται δυνάμεις τριβής στο εσωτερικό τους.Αυτές οι δυνάμεις τριβής αντιτίθενται στην κίνηση ενός τμήματος του ρευστού ως προς ένα άλλο τμήμα του.
Όμως για πραγματικά ρευστά οι δυνάμεις τριβής υπάρχουν.Αυτές οι δυνάμεις έχουν πολύ σημαντικές πρακτικές εφαρμογές.Για παράδειγμα η λίπανση των τμημάτων μιας μηχανής θα ήταν αδύνατη αν το λιπαντικό δεν παρουσίαζε κατά τη ροή του τέτοιες δυνάμεις τριβής.
.jpg) |
| Οι δυνάμεις τριβής αντιτίθενται στην κίνηση ενός τμήματος του ρευστού ως προς ένα άλλο τμήμα του |
 |
| Αυτή η αντίσταση στην κίνηση στρωμάτων του ρευστού είναι ένα είδος εσωτερικής τριβής,που ονομάζεται ιξώδες |
 |
| Στην περίπτωση των υγρών το ιξώδες οφείλεται στη δύναμη τριβής ανάμεσα σε παρακείμενα στρώματα του ρευστού καθώς αυτά ολισθαίνουν το ένα πάνω στο άλλο |
Από το ακόλουθο παράδειγμα μπορούμε να καταλάβουμε καλύτερα το μέγεθος του ιξώδους ενός ρευστού.Παίρνουμε δυο τζάμια,στερεώνουμε καλά το ένα πάνω στο άλλο και αλείφουμε την πάνω επιφάνεια του με λάδι.Τοποθετούμε το δεύτερο τζάμι επάνω στο πρώτο και το κινούμε ελαφρά.Θα δούμε ότι ολισθαίνει με ευκολία.Εάν όμως αντί για λάδι βάλουμε πίσσα ανάμεσα στα δυο τζάμια,θα δούμε ότι είναι δυσκολότερο να κινήσουμε το ένα τζάμι πάνω στο άλλο.Συμπεραίνουμε λοιπόν ότι η πίσσα έχει μεγαλύτερο ιξώδες από ότι το λάδι.
ΔΙΑΤΜΗΤΙΚΗ ΤΑΣΗ
Στη μηχανική των ρευστών διατμητική τάση ονομάζεται η δύναμη που συνηθέστερα παραμορφώνει τα ρευστά στη ροή τους,ανεξάρτητα το πόσο μικρή μπορεί να είναι.
 |
| Στη μηχανική των ρευστών διατμητική τάση ονομάζεται η δύναμη που συνηθέστερα παραμορφώνει τα ρευστά στη ροή τους,ανεξάρτητα το πόσο μικρή μπορεί να είναι |
Ας θυμηθούμε ότι σε ένα στερεό που υπόκειται σε διατμητική τάση τα παρακείμενα στρώματα μετατοπίζονται το ένα ως προς το άλλο.Κατά αναλογία,όταν τα παρακείμενα στρώματα ενός ρευστού υφίσταται διατμητική τάση,κινούνται το ένα ως προς το άλλο.Θεωρούμε ότι από τα δυο στρώματα το ένα είναι ακίνητο,ενώ το άλλο κινείται προς τα δεξιά υπό την επίδραση μιας εξωτερικής δύναμης F.
 |
| Εφαρμογή διατμητικής τάσης στην κορυφή του ορθογωνίου ενώ η βάση παραμένει σταθερή.Η διατμητική τάση που προκύπτει παραμορφώνει το ορθογώνιο σε ένα παραλληλόγραμμο |
Ως διατμητική τάση χαρακτηρίζεται το πηλίκο της παράλληλης ή εφαπτομενικής δύναμης που εφαρμόζεται σε μια επιφάνεια ρευστού,προς το εμβαδόν της επιφάνειας αυτής.
 |
| Ως διατμητική τάση χαρακτηρίζεται το πηλίκο της παράλληλης ή εφαπτομενικής δύναμης που εφαρμόζεται σε μια επιφάνεια ρευστού,προς το εμβαδόν της επιφάνειας αυτής |
Άρα εξ ορισμού,η διατμητική τάση ισούται με τον λόγο F/A:
τ=F/A
όπου:
τ η διατμητική τάση,
F η παράλληλη συνιστώσα της δύναμης εφαρμογής,
Α η επιφάνεια εφαρμογής.
Μονάδα μέτρησης της διατμητικής τάσης στο Διεθνές Σύστημα Μονάδων (SI) είναι το ένα πασκάλ 1 Ρα που είναι ίσο με 1 Νιούτον (μονάδα ασκούμενης δύναμης) ανά τετραγωνικό μέτρο (μέτρο επιφάνειας εφαρμογής στο SI):
1 Ρα=1 Ν/m2
Συνέπεια του παραπάνω ορισμού είναι ότι κάθε ρευστό (υγρό ή αέριο) που βρίσκεται σε ισορροπία δε δέχεται διατμητική τάση.
Η διατμητική τάση εφαρμόζεται εφαπτομενικά σε αντίθεση με την πίεση που εφαρμόζεται κάθετα στην επιφάνεια του ρευστού.
Η διατμητική τάση εφαρμόζεται εφαπτομενικά σε αντίθεση με την πίεση που εφαρμόζεται κάθετα στην επιφάνεια του ρευστού.
ΔΙΑΤΜΗΤΙΚΗ ΠΑΡΑΜΟΡΦΩΣΗ
Μετά από μικρό χρονικό διάστημα,μέρος του υγρού έχει παραμορφωθεί λόγω αυτής της κίνησης και το αρχικό σχήμα έχει μεταβληθεί.Το υγρό έχει υποστεί διατμητική παραμόρφωση.
Εξ ορισμού η διατμητική παραμόρφωση ισούται με τον λόγο Δx/l:
Επομένως:
γ=Δx/l
όπου:
γ η διατμητική παραμόρφωση,
Δx η απόσταση που μετατοπίστηκε το ρευστό,
l το πάχος του ρευστού.
l το πάχος του ρευστού.
 |
| Η διατμητική παραμόρφωση ισούται με τον λόγο Δx/l |
Η επάνω πλάκα και το παρακείμενο της υγρό κινούνται με μέτρο ταχύτητας υ.Δηλαδή στο χρονικό διάστημα Δt το υγρό δίπλα στην επάνω πλάκα μετατοπίστηκε κατά απόσταση Δx=υ·Δt.
Η διατμητική παραμόρφωση ανά μονάδα χρόνου είναι:
γ/Δt=Δx/l/Δt=υ/l
Η εξίσωση αυτή λέει ότι ο ρυθμός μεταβολής της διατμητικής παραμόρφωσης είναι υ/l.
Τώρα αντικαθιστούμε το μέλι με ένα άλλο ρευστό που ρέει ευκολότερα,για παράδειγμα το λάδι.Διαπιστώνουμε ότι η δύναμη που πρέπει να ασκούμε στην πάνω πλάκα για να διατηρείται η ταχύτητά της σταθερή είναι μικρότερη.Επίσης η δύναμη είναι μικρότερη εάν,για το ίδιο ρευστό,μεταξύ των πλακών αυξήσουμε το πάχος του l.
Αντίθετα η δύναμη γίνεται μεγαλύτερη αν οι επιφάνειες των πλακών είναι μεγαλύτερες ή αν επιχειρήσουμε να μετακινήσουμε την πάνω πλάκα με μεγαλύτερη ταχύτητα.
ΕΣΩΤΕΡΙΚΗ ΤΡΙΒΗ ΜΕΣΑ ΣΕ ΕΝΑ ΥΓΡΟ
Θεωρούμε δύο γυάλινες οριζόντιες πλάκες εμβαδού Α όπως φαίνεται στο παρακάτω σχήμα.Σταθεροποιούμε την κάτω πλάκα και απλώνουμε πάνω της ένα στρώμα από μέλι πάχους l.Μετά τοποθετούμε τη δεύτερη πλάκα πάνω στο μέλι και τη μετακινούμε με σταθερή ταχύτητα υ σε σχέση με την κάτω ακίνητη πλάκα.Διαπιστώνουμε ότι για να συνεχιστεί η κίνηση απαιτείται να ασκηθεί κάποια δύναμη F.Η δύναμη αυτή απαιτείται για να αντισταθμίσει τις τριβές (ιξώδες),που αναπτύσσονται μεταξύ των στρωμάτων του μελιού που κινούνται το ένα σε σχέση με το άλλο.
.jpg) |
| Στρώμα υγρού που περιέχεται μεταξύ δύο γυάλινων οριζόντιων πλακών,από τις οποίες η κάτω είναι ακίνητη ενώ η επάνω κινείται με ταχύτητα υ |
Βλέπουμε ότι το ανώτερο στρώμα έχει προσκολληθεί στην πάνω πλάκα και κινείται με ταχύτητα υ ενώ το κατώτερο έχει προσκολληθεί στην κάτω πλάκα και παραμένει ακίνητο.Όλα τα ενδιάμεσα στρώματα έχουν ταχύτητες διαφορετικές μεταξύ τους, που αυξάνουν σταδιακά από 0 έως υ καθώς πηγαίνουμε από την κάτω πλάκα προς την πάνω.
.jpg) |
| Διάγραμμα ταχυτήτων για ένα ρευστό σε κυλινδρικό σωλήνα ακτίνας R |
 |
| Ιξώδες |
 |
| Το ιξώδες μετριέται με ειδικό όργανο που λέγεται ιξωδόμετρο |
Μπορούμε να αποδείξουμε ότι το μέτρο της δύναμης F δίνεται από τη σχέση:
F=n·Α·υ/l
F=n·Α·υ/l
Το ιξώδες μετριέται με ειδικό όργανο που λέγεται ιξωδόμετρο.
ΣΥΝΤΕΛΕΣΤΗΣ ΙΞΩΔΟΥΣ
Ορίζουμε ότι ο συντελεστής ιξώδους (ή εσωτερικής τριβής),η,του ρευστού ισούται με το λόγο της διατμητικής τάσης προς τον ρυθμό μεταβολής της διατμητικής παραμόρφωσης:
n=F/Α/υ/l=F·l/Α·υ
O συντελεστής ιξώδους n είναι χαρακτηριστικός κάθε ρευστού.
 |
| Ορίζουμε ότι ο συντελεστής ιξώδους (ή εσωτερικής τριβής),η,του ρευστού ισούται με το λόγο της διατμητικής τάσης προς τον ρυθμό μεταβολής της διατμητικής παραμόρφωσης |
1 Ν·s/m2
Στο παρακάτω πίνακα θα βρούμε τον συντελεστή ιξώδους για διάφορα ρευστά.
| Ρευστό | θ (οC) | Συντελεστής ιξώδους η (Ν s/m2) |
| Νερό | 20 | 1,0 x10-3 |
| Νερό | 100 | 0,3 x10-3 |
| Αίμα | 37 | 2,7 x10-3 |
| Γλυκερίνη | 20 | 830 x10-3 |
| Μηχανέλαιο (δεκάρι) | 30 | 250 x10-3 |
ΝΕΥΤΩΝΕΙΑ ΡΕΥΣΤΑ
 |
| Νευτώνεια ρευστά ονομάζονται τα ρευστά που υπακούουν στην εξίσωση n=F·l/Α·υ |
 |
| Το αίμα είναι ένα αιώρημα στερεών σωματιδίων μέσα σε υγρό.Καθώς αυξάνει η ταχύτητα ροής τα σωματίδια παραμορφώνονται και προσανατολίζονται με τέτοιο τρόπο ώστε να διευκολύνουν τη ροή |
Το αίμα παρουσιάζει κάποια ενδιαφέρουσα ιδιαιτερότητα.Το αίμα είναι ένα αιώρημα στερεών σωματιδίων μέσα σε υγρό.Καθώς αυξάνει η ταχύτητα ροής,για να μην αυξηθούν υπέρμετρα οι εσωτερικές τριβές,τα σωματίδια παραμορφώνονται και προσανατολίζονται με τέτοιο τρόπο ώστε να διευκολύνουν τη ροή.
ΜΗ ΝΕΥΤΩΝΕΙΑ ΡΕΥΣΤΑ
Στο σημείο αυτό πρέπει να επισημάνουμε ότι δεν υπακούουν όλα τα ρευστά στην εξίσωση.Δεν υπάρχει σε όλα τα ρευστά γραμμική αναλογία ανάμεσα στην εσωτερική τριβή που παρουσιάζουν κατά τη ροή τους και την ταχύτητα ροής.
 |
| Μη νευτώνεια ρευστά |
Η παραπάνω εξίσωση που ορίζει τον συντελεστή ιξώδους η ισχύει μόνον εάν το μέτρο της ταχύτητας μεταβάλλεται γραμμικά συναρτήσει του πάχους του ρευστού.Τότε λέμε ότι ο ρυθμός μεταβολής της ταχύτητας συναρτήσει του πάχους είναι σταθερός.Εάν δεν είναι,τότε πρέπει να χρησιμοποιήσουμε τον γενικό τύπο του η:
n=F/Α/dυ/dy
Αυτά τα ρευστά ονομάζονται μη νευτώνεια ρευστά.
 |
| Τα μη νευτώνεια ρευστά χαρακτηρίζονται συνήθως υγρά που παρουσιάζουν μικρότερης κλίμακας ιδιότητες των φυσικών ρευστών,δηλαδή χαμηλό ιξώδες |
Τέτοια χαρακτηρίζονται συνήθως υγρά που παρουσιάζουν μικρότερης κλίμακας ιδιότητες των φυσικών ρευστών,δηλαδή χαμηλό ιξώδες ιδιαίτερα όταν υποβάλλονται σε ανάδευση και γίνονται περισσότερο λεπτόρρευστα,όπως,για παράδειγμα,το τυπογραφικό μελάνι,οι διάφορες βαφές (ελαιοχρώματα κ.λπ.).
 |
| Στα μη νευτώνεια ρευστά υπάγονται τα πυκνά αιωρήματα |
Επίσης σ΄ αυτή τη κατηγορία υπάγονται τα πυκνά αιωρήματα καθώς και τα διάφορα πυκνά γαλακτώματα.
ΑΡΙΘΜΟΣ ΤΟΥ REYNOLDS
Όταν τα παρακείμενα στρώματα ενός ρευστού με ιξώδες ρέουν στρωτά το ένα πάνω στο άλλο,αυτή η σταθερή ροή ονομάζεται στρωτή ροή.
Σε μεγάλες όμως ταχύτητες η ροή του ρευστού μεταβάλλεται και από στρωτή ροή γίνεται τελείως ακανόνιστη και τυχαία,οπότε ονομάζεται τυρβώδης ροή.Η ταχύτητα κατά την οποία αρχίζει η τυρβώδης ροή εξαρτάται από το ιξώδες του ρευστού και από την γεωμετρία του περιβάλλοντος μέσου.
Μπορούμε να δώσουμε πολλά παραδείγματα τυρβώδους ροής.Το νερό ενός ρυακιού που έχει πολλές πέτρες και ο καπνός που βγαίνει από τους καπνοδόχους ρέουν τυρβωδώς.Επίσης τα απόνερα ενός ταχύπλοου σκάφους και ο αέρας πίσω από ένα αεροπλάνο κινούνται τυρβωδώς.
Έχει διαπιστωθεί από διάφορα πειράματα ότι η αρχή της τυρβώδους ροής προσδιορίζεται από μια παράμετρο που ονομάζεται αριθμός του Reynolds,ο οποίος ισούται με:
RN=ρ·υ·d/η
όπου:
RN ο αριθμός του Reynolds,
ρ η πυκνότητα του ρευστού,
υ το μέτρο της ταχύτητας του ρευστού,
d ένα χαρακτηριστικό μήκος που έχει σχέση με την ροή,
η ο συντελεστής ιξώδους του ρευστού.
Για ροή δια μέσου ενός σωλήνα το d ισούται με τη διάμετρο του σωλήνα ενώ για τη περίπτωση ροής γύρω από σφαίρα το d ισούται με τη διάμετρο της σφαίρας.
Από διάφορα πειράματα γνωρίζουμε ότι εάν ο αριθμός του Reynolds είναι μικρότερος από 2.000,τότε η ροή είναι στρωτή.Εάν ο αριθμός του Reynolds είναι μεγαλύτερος από 3.000,η ροή είναι τυρβώδες.
ΑΡΙΘΜΟΣ ΤΟΥ REYNOLDS
Όταν τα παρακείμενα στρώματα ενός ρευστού με ιξώδες ρέουν στρωτά το ένα πάνω στο άλλο,αυτή η σταθερή ροή ονομάζεται στρωτή ροή.
Σε μεγάλες όμως ταχύτητες η ροή του ρευστού μεταβάλλεται και από στρωτή ροή γίνεται τελείως ακανόνιστη και τυχαία,οπότε ονομάζεται τυρβώδης ροή.Η ταχύτητα κατά την οποία αρχίζει η τυρβώδης ροή εξαρτάται από το ιξώδες του ρευστού και από την γεωμετρία του περιβάλλοντος μέσου.
 |
| Η περίπτωση ροής γύρω από σφαίρα |
Έχει διαπιστωθεί από διάφορα πειράματα ότι η αρχή της τυρβώδους ροής προσδιορίζεται από μια παράμετρο που ονομάζεται αριθμός του Reynolds,ο οποίος ισούται με:
RN=ρ·υ·d/η
όπου:
RN ο αριθμός του Reynolds,
ρ η πυκνότητα του ρευστού,
υ το μέτρο της ταχύτητας του ρευστού,
d ένα χαρακτηριστικό μήκος που έχει σχέση με την ροή,
η ο συντελεστής ιξώδους του ρευστού.
 |
| Η ποιοτική συμπεριφορά της ροής ρευστού σε ένα κύλινδρο εξαρτάται σε μεγάλο βαθμό από τον αριθμό Reynolds |
Από διάφορα πειράματα γνωρίζουμε ότι εάν ο αριθμός του Reynolds είναι μικρότερος από 2.000,τότε η ροή είναι στρωτή.Εάν ο αριθμός του Reynolds είναι μεγαλύτερος από 3.000,η ροή είναι τυρβώδες.





.JPG)
.jpg)
.JPG)
.jpg)
.jpg)
.jpg)
.JPG)
.JPG)
.jpg)
.JPG)
.JPG)
.jpg)
.JPG)
.JPG)
.JPG)

.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)




