ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ
Για να κατασκευάσουμε μια γραφική παράσταση μιας συνάρτησης μας χρειάζεται ένας πίνακας τιμών.Ο πίνακας αυτός μπορεί να προέλθει είτε από πειραματικές μετρήσεις φυσικών μεγεθών,είτε από αυθαίρετες τιμές που δίνουμε στην ανεξάρτητη μεταβολή μέσα στο πεδίο ορισμού της, όπως φαίνεται στα παρακάτω παραδείγματα α,β και γ.
Μετά τη δημιουργία του πίνακα τιμών προχωρούμε στην κατασκευή και βαθμολόγηση των αξόνων x,y,σύμφωνα με τις τιμές που έχουν τα φυσικά μεγέθη.Αν η συνάρτηση ή η σχέση είναι πρώτου βαθμού,η γραφική παράσταση θα είναι ευθεία γραμμή και αρκούν δύο σημεία για τον προσδιορισμό της.Αν η συνάρτηση είναι τριώνυμο δευτέρου βαθμού τότε η γραφική παράσταση είναι παραβολή.Για παράδειγμα αναφέρουμε τις τρεις παρακάτω περιπτώσεις:
α) Η γραφική παράσταση της συνάρτησης y=2x+4,x ϵ [0,5] είναι:
 |
| ΓΡΑΦΙΚΕΣ ΠΑΡΑΣΤΑΣΕΙΣ |
.jpg) |
| Άξονα x-y |
.jpg) |
| Μετά τη δημιουργία του πίνακα τιμών προχωρούμε στην κατασκευή και βαθμολόγηση των αξόνων x,y,σύμφωνα με τις τιμές που έχουν τα φυσικά μεγέθη |
Πίνακας τιμών
x
|
y
|
0
5
|
4
14
|
Ως κλίση της ευθείας ορίζεται το πηλίκο που προκύπτει από το τρίγωνο της Εικόνας:
Δy/Δx=10/5=2
και είναι ίση με τον συντελεστή του x της συνάρτησης y=2x+4.
β) Η γραφική παράσταση της σχέσης m=6V είναι:
Πίνακας τιμών
m(g)
|
V(cm3)
|
0
10
|
0
60
|
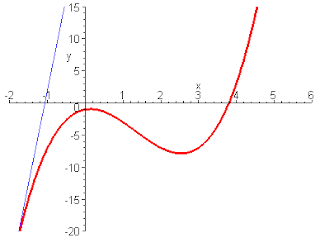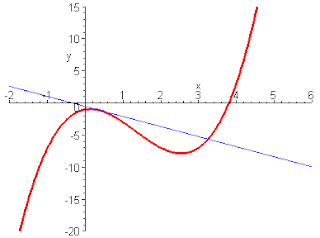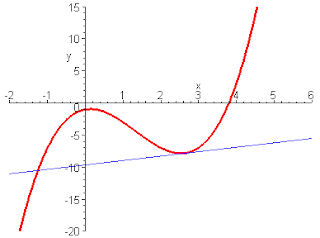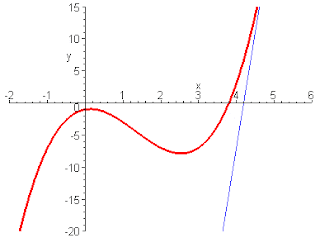
γ) Η γραφική παράσταση της συνάρτησης x=2t+t2,t ϵ[0,4]
Μπορούμε να βρούμε την κλίση της καμπύλης όπως στην περίπτωση της ευθείας γραμμής;
Μήπως η καμπύλη δεν έχει μια κλίση,αλλά κάθε σημείο της έχει τη δική του κλίση;
Πίνακας τιμών
t
|
x
|
0
1
2
3
4
|
0
3
8
15
24
|
Πράγματι κάθε σημείο της έχει κλίση που βρίσκεται αν φέρουμε την εφαπτομένη της καμπύλης στο σημείο αυτό,όπως φαίνεται στην εικόνα γ,και φτιάξουμε ένα οποιοδήποτε ορθογώνιο τρίγωνο με υποτείνουσα τμήμα της εφαπτόμενης που φέραμε,π.χ. η κλίση του σημείου 1 είναι:
Δy/Δx =9/1,7=5,3





.jpg)
.jpg)
.jpg)

