ΘΕΩΡΗΜΑ TORRICELLI (ΤΟΡΙΚΕΛΙ)
Εφαρμόζουμε το νόμο του Bernoulli για τις θέσεις Ε (ελεύθερη επιφάνεια) και Κ (στόμιο εκροής):
pΕ+1/2·ρ·υΕ2+ρ·g·h=pΚ+1/2·ρ·υκ2+0
pΕ=pΚ=pαt
Η ταχύτητα με την οποία κατεβαίνει η στάθμη του υγρού μπορεί να θεωρηθεί αμελητέα συγκριτικά με την ταχύτητα με την οποία ρέει το νερό στο Κ:
υΕ=0
που αποτελεί τη μαθηματική έκφραση του θεωρήματος του Torricelli (Τορικέλι) που το διατύπωσε το 1644 ο Evangelista Torricelli.
ΧΡΟΝΟΣ ΓΙΑ ΝΑ ΑΔΕΙΑΣΕΙ ΤΟ ΔΟΧΕΙΟ
Θεωρούμε να δοχείο που περιέχει νερό και αδειάζει ελεύθερα μέσω ενός σωλήνα.Έστω h το ύψος του νερού σε οποιαδήποτε στιγμή.
Έχουμε:
Α·dh=α·dx
όπου:
Α το εμβαδόν της ελεύθερης επιφάνειας,
α το εμβαδόν της διατομής εκροής,
dh το ύψος του υγρού στο δοχείο,
dx το μήκος του σωληνάριου σε χρόνο dt.



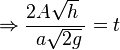

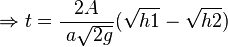
είναι ο χρόνος που απαιτείται για να αδειάσει το νερό δοχείου από το ύψος h1 μέχρι το ύψος h2.
 |
| ΘΕΩΡΗΜΑ TORRICELLI (ΤΟΡΙΚΕΛΙ) |
ΕΙΣΑΓΩΓΗ
Το Θεώρημα του Τοριτσέλι προσδιορίζει την εκροή ιδεώδους ρευστού στο ελεύθερο αέρα.Προϋπόθεση ισχύος του θεωρήματος αυτού είναι το εμβαδόν διατομής εκροής να είναι κατά πολύ μικρότερο της ελεύθερης επιφάνειας.
Το Θεώρημα του Τοριτσέλι προσδιορίζει την εκροή ιδεώδους ρευστού στο ελεύθερο αέρα.Προϋπόθεση ισχύος του θεωρήματος αυτού είναι το εμβαδόν διατομής εκροής να είναι κατά πολύ μικρότερο της ελεύθερης επιφάνειας.
Ο νόμος ανακαλύφθηκε (αν και όχι σε αυτή τη μορφή) από την Ιταλό επιστήμονα Evangelista Torricelli,το 1644.Αργότερα αποδείχθηκε ότι είναι μια ειδική περίπτωση της αρχής του Bernoulli.
ΜΑΘΗΜΑΤΙΚΗ ΕΚΦΡΑΣΗ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ ΤΟΥ TORRICELLI
Θεωρούμε το δοχείο του παρακάτω σχήματος στη βάση του οποίου υπάρχει στόμιο εκροής.Θα υπολογίσουμε την ταχύτητας εκροής υγρού του ανοικτού δοχείου.
ΜΑΘΗΜΑΤΙΚΗ ΕΚΦΡΑΣΗ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ ΤΟΥ TORRICELLI
Θεωρούμε το δοχείο του παρακάτω σχήματος στη βάση του οποίου υπάρχει στόμιο εκροής.Θα υπολογίσουμε την ταχύτητας εκροής υγρού του ανοικτού δοχείου.
.jpg) |
| Θεωρούμε το δοχείο στη βάση του οποίου υπάρχει στόμιο εκροής.Θέλουμε να υπολογίσουμε την ταχύτητας εκροής υγρού του ανοικτού δοχείου |
pΕ+1/2·ρ·υΕ2+ρ·g·h=pΚ+1/2·ρ·υκ2+0
Η πίεση τόσο στην ελεύθερη επιφάνεια όσο και στο σημείο εξόδου είναι η ατμοσφαιρική,δηλαδή:
pΕ=pΚ=pαt
Η ταχύτητα με την οποία κατεβαίνει η στάθμη του υγρού μπορεί να θεωρηθεί αμελητέα συγκριτικά με την ταχύτητα με την οποία ρέει το νερό στο Κ:
Λαμβάνοντας υπόψη τις δυο τελευταίες σχέσεις και επιλύοντας την πρώτη ως προς υκ βρίσκουμε:
υκ=(2·g·h)1/2
που αποτελεί τη μαθηματική έκφραση του θεωρήματος του Torricelli (Τορικέλι) που το διατύπωσε το 1644 ο Evangelista Torricelli.
 |
| Το θεώρημα του Torricelli (Τορικέλι) |
Την ίδια χρονιά ο Evangelista Torricelli ανακάλυψε το υδραργυρικό βαρόμετρο.
ΔΙΑΤΥΠΩΣΗ ΤΟΥ ΘΕΩΡΗΜΑΤΟΣ ΤΟΥ TORRICELLI
Το θεώρημα του Torricelli (Τορικέλι) διατυπώνεται ως εξής:
Η ταχύτητα εκροής υγρού από στόμιο που βρίσκεται σε βάθος h από την ελεύθερη επιφάνειά του είναι ίση με την ταχύτητα που θα είχε το υγρό αν έπεφτε ελεύθερα από ύψος h.
Το θεώρημα του Torricelli (Τορικέλι) διατυπώνεται ως εξής:
Η ταχύτητα εκροής υγρού από στόμιο που βρίσκεται σε βάθος h από την ελεύθερη επιφάνειά του είναι ίση με την ταχύτητα που θα είχε το υγρό αν έπεφτε ελεύθερα από ύψος h.
.jpg) |
| Η ταχύτητα εκροής υγρού από στόμιο που βρίσκεται σε βάθος h από την ελεύθερη επιφάνειά του είναι ίση με την ταχύτητα που θα είχε το υγρό αν έπεφτε ελεύθερα από ύψος h |
Αργότερα αποδείχθηκε ότι είναι μια ειδική περίπτωση της αρχής του Bernoulli.
Θεωρούμε να δοχείο που περιέχει νερό και αδειάζει ελεύθερα μέσω ενός σωλήνα.Έστω h το ύψος του νερού σε οποιαδήποτε στιγμή.
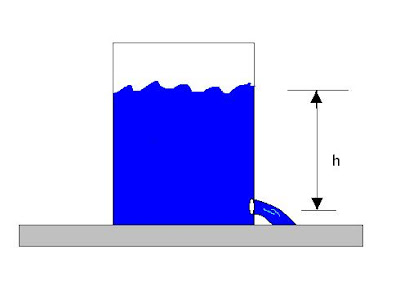 |
| Θεωρούμε να δοχείο που περιέχει νερό και αδειάζει ελεύθερα μέσω ενός σωλήνα.Έστω h το ύψος του νερού σε οποιαδήποτε στιγμή |
Η ταχύτητα εκροής είναι:
Έχουμε:
Α·dh=α·dx
όπου:
Α το εμβαδόν της ελεύθερης επιφάνειας,
α το εμβαδόν της διατομής εκροής,
dh το ύψος του υγρού στο δοχείο,
dx το μήκος του σωληνάριου σε χρόνο dt.



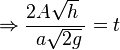

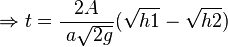
είναι ο χρόνος που απαιτείται για να αδειάσει το νερό δοχείου από το ύψος h1 μέχρι το ύψος h2.





.jpg)


