ΝΟΜΟΣ ΣΥΝΕΧΕΙΑΣ

ΝΟΜΟΣ ΣΥΝΕΧΕΙΑΣ

ΝΟΜΟΣ ΣΥΝΕΧΕΙΑΣ

ΕΙΣΑΓΩΓΗ

 Ο Νόμος της συνέχειας της ροής είναι από τους σημαντικότερους νόμους στην Υδροδυναμική.
 Η σχέση που περιγράφει αυτόν τον νόμο ονομάζεται εξίσωση της συνέχειας της ροής και είναι άμεση συνέπεια της αρχής διατήρησης της ύλης.

Η παροχή παραμένει σταθερή κατά μήκος μίας φλέβας (ενός σωλήνα),που διαρρέεται από υγρό

 Η αρχή αυτή προέρχεται από το γεγονός ότι η μάζα διατηρείται πάντα σε υγρά συστήματα ανεξάρτητα από την πολυπλοκότητα του αγωγού ή την κατεύθυνση της ροής.
 Αναφέρει ότι η παροχή παραμένει σταθερή κατά μήκος μίας φλέβας ή ενός σωλήνα,που διαρρέεται από υγρό.

ΕΞΙΣΩΣΗ ΣΥΝΕΧΕΙΑΣ

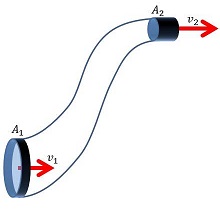
 Θεωρούμε ότι η ροή ενός ρευστού γίνεται  σ' ένα σωλήνα μεταβλητής διατομής.Τα μόρια του ρευστού κινούνται παράλληλα από τις δυναμικές γραμμές υπό συνθήκες στρωτής ροής.

 Σε όλα τα σημεία οι ταχύτητες των μορίων εφάπτονται των αντίστοιχων ρευματικών γραμμών τις οποίες ακολουθούν.

Θεωρούμε ότι η ροή ενός ρευστού γίνεται σ' ένα σωλήνα μεταβλητής διατομής

 Θεωρούμε ένα ασυμπίεστο ρευστό που ρέει μέσα στο σωλήνα της μεταβλητής διατομής.

 Στο μικρό χρονικό διάστημα Δt το ρευστό στο αριστερό μέρος του σωλήνα κινείται διανύοντας απόσταση: 

                                                                                      Δx1=υ1·Δt

όπου:

Δx1 η απόσταση που διανύει το ρευστό στο αριστερό μέρος του σωλήνα,στο μικρό χρονικό διάστημα Δt,

υ1 η ταχύτητα του ρευστού στην διατομή Α1,

Δt το μικρό χρονικό διάστημα.

Στο μικρό χρονικό διάστημα Δt το ρευστό στο αριστερό μέρος του σωλήνα κινείται διανύοντας απόσταση Δx1=υ1·Δt

 Αν ΔV1 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm1 και Α1 η διατομή του σωλήνα στην περιοχή αυτήν,τότε η μάζα που ρέει στην ίδια περιοχή είναι:  

                                                                                      Δm1=ρ·ΔV1

όπου:

Δm1 η στοιχειώδης μάζα που ρέει στην ίδια περιοχή στο αριστερό μέρος του σωλήνα,

ρ η πυκνότητα του ρευστού,

ΔV1 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm1.

 Όμως:  

ΔV1=A1·Δx1=A1·υ1·Δt 

  Άρα:

                                                                Δm1=ρ·ΔV1=ρ·Α1·Δx1=ρ·Α1·υ1·Δt

 Παρομοίως στο ίδιο μικρό χρονικό διάστημα Δt το ρευστό στο δεξιό μέρος του σωλήνα κινείται διανύοντας απόσταση: 

                                                                                      Δx2=υ2·Δt

όπου:

Δx2 η απόσταση που διανύει το ρευστό στο αριστερό μέρος του σωλήνα,στο μικρό χρονικό διάστημα Δt,

υ2 η ταχύτητα του ρευστού στην διατομή Α1,

Δt το μικρό χρονικό διάστημα.

Σε σημεία όπου ο σωλήνας στενεύει η ταχύτητα ροής είναι πιο μεγάλη

 Αν ΔV2 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm2 και Α2 η διατομή του σωλήνα στην περιοχή αυτήν,τότε η μάζα που ρέει στην ίδια περιοχή είναι:  

                                                                                      Δm2=ρ·ΔV2

όπου:

Δm2 η στοιχειώδης μάζα που ρέει στην ίδια περιοχή στο δεξιό  μέρος του σωλήνα,

ρ η πυκνότητα του ρευστού,

ΔV2 ο στοιχειώδης όγκος που καταλαμβάνει μέσα στο σωλήνα η μάζα Δm2.

Το μέτρο της ταχύτητας του ρευστού είναι μεγάλο εκεί όπου ο σωλήνας είναι στενός και μικρό εκεί όπου ο σωλήνας είναι φαρδύς  

 Όμως:

ΔV2=A2·Δx2=A2·υ2·Δt 

 Άρα:

                                                                Δm2=ρ·ΔV2=ρ·Α2·Δx2=ρ·Α2·υ2·Δt

 Όμως το ρευστό θεωρείται ασυμπίεστο που σημαίνει ότι η πυκνότητα του είναι ίδια σε όλη την έκταση του.

Η ποσότητα που εισέρχεται στον σωλήνα στο χρονικό διάστημα Δt είναι ίση με την ποσότητα που εξέρχεται από τον σωλήνα στο ίδιο χρονικό διάστημα

 Γνωρίζουμε όμως ότι η μάζα διατηρείται και επειδή έχουμε στρωτή ροή,θα πρέπει η μάζα Δm1 που περνάει από τη διατομή Α1 του σωλήνα στο χρονικό διάστημα Δt να είναι ίση με τη μάζα Δm2 που περνάει από μία άλλη διατομή του σωλήνα Α2 στο ίδιο χρονικό διάστημα Δt.
 Είναι:

                                                                                      Δm1=Δm2           ή 

                                                                                     ρ·ΔV1=ρ·ΔV2          ή

                                                                                  ρ·Α1·Δx1=ρ·Α2·Δx2        ή

                                                                            ρ·A1·υ1·Δt=ρ·A2·υ2·Δt     ή 

και τελικά:

                                                                                         A1·υ1=A2·υ2

 Η εξίσωση αυτή ονομάζεται εξίσωση της συνέχειας.

Η εξίσωση A1·υ1=A2·υ2 ονομάζεται εξίσωση της συνέχειας και είναι άμεση συνέπεια της αρχής διατήρησης της ύλης

 Άρα η εξίσωση της συνέχειας διατυπώνεται ως εξής:

 Για όλα τα σημεία ενός σωλήνα ή μιας φλέβας το γινόμενο της επιφάνειας διατομής επί την ταχύτητα του ρευστού είναι σταθερό.

 Άρα το μέτρο της ταχύτητας του ρευστού είναι μεγάλο εκεί όπου ο σωλήνας είναι στενός και μικρό εκεί όπου ο σωλήνας είναι φαρδύς.

Για όλα τα σημεία του σωλήνα ή της φλέβας το γινόμενο της επιφάνειας διατομής επί την ταχύτητα του ρευστού είναι σταθερό

 Η εξίσωση της συνέχειας είναι άμεση συνέπεια της αρχής διατήρησης της ύλης.

Η εξίσωση της συνέχειας είναι άμεση συνέπεια της αρχής διατήρησης της ύλης

 Η εξίσωση της συνέχειας ισοδυναμεί με το γεγονός ότι η ποσότητα που εισέρχεται στον σωλήνα στο χρονικό διάστημα Δt είναι ίση με την ποσότητα που εξέρχεται από τον σωλήνα στο ίδιο χρονικό διάστημα.

ΝΟΜΟΣ ΣΥΝΕΧΕΙΑΣ

 Η παροχή σωλήνα ή φλέβας σε κάποια θέση είναι ίση με το γινόμενο του εμβαδού της διατομής επί την ταχύτητα του ρευστού στη θέση αυτή.

                                                                                Π=Α·υ 

 Άρα η εξίσωση της συνέχειας γράφεται και:  

                                                                                Π1=Π2                        ή  
                                                                                  
                                                                                Π=σταθερό                

  Η σχέση Π=σταθερό ισχύει για σωλήνα αλλά και για φλέβα και διατυπώνεται ως εξής:

 Κατά μήκος ενός σωλήνα ή μιας φλέβας η παροχή διατηρείται σταθερή.

 Η διατύπωση αυτή ονομάζεται Νόμος της συνέχειας της ροής.

Κατά μήκος ενός σωλήνα ή μιας φλέβας η παροχή διατηρείται σταθερή

 Ο Νόμος της συνέχειας της ροής είναι από τους σημαντικότερους νόμους στην Υδροδυναμική.

 Από τη σχέση  A1·υ1=A2·υ2 φαίνεται ότι κατά μήκος ενός σωλήνα που δεν έχει σταθερή διατομή,η ταχύτητα του υγρού δεν είναι παντού ίδια.Σε σημεία όπου ο σωλήνας στενεύει η ταχύτητα ροής είναι πιο μεγάλη.

Η ταχύτητα ροής είναι μεγαλύτερη εκεί που πυκνώνουν οι ρευματικές γραμμές

 Κατά μήκος ενός ποταμού με σταθερό πλάτος πολλές φορές το βάθος ποικίλει.Όπου το ποτάμι έχει μικρό βάθος έχει και μικρή εγκάρσια διατομή.

Επειδή η παροχή είναι σταθερή,στις περιοχές όπου το ποτάμι είναι ρηχό το νερό κυλάει γρηγορότερα

 Επειδή η παροχή είναι σταθερή,στις περιοχές όπου το ποτάμι είναι ρηχό το νερό κυλάει γρηγορότερα.Μπορούμε να πούμε ότι εκεί που οι ρευματικές γραμμές πυκνώνουν η ταχύτητα ροής είναι πιο μεγάλη.